"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРАНИЧНЫЕ СВОЙСТВА АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Значение ГРАНИЧНЫЕ СВОЙСТВА АНАЛИТИЧЕСКИХ ФУНКЦИЙ в математической энциклопедии:
- свойства аналитич. функций, проявляющиеся при приближении к границе области определения.
Можно считать, что понимаемое в самом широком смысле изучение Г. с. а. ф. началось с Сохоцкого теоремы и Пикара теоремы о поведении аналнтич. функций в окрестности изолированной существенно особой точки, полученных во 2-й пол. 19 в. В лекциях П. Пенлеве (P.Painleve, 1895) впервые появляются термины того подхода к изучению Г. с. а. ф., к-рый теперь носит назв. теории предельных множеств. В диссертации П. Фату (P. Fatou, 1906) впервые систематически изучаются нек-рые Г. с. а. ф. вблизи непрерывной границы области определения. Примерно в 1-й трети 20 в. теория Г. с. а. ф. получила существенное развитие в трудах многих ученых. После середины 20 в. теория Г. с. а. ф. снова развивается очень бурно, в ней возникают новые идеи и методы, новые направления и объекты исследования. В своем развитии теория Г. с. а. ф. тесно взаимодействует с различными областями математического анализа и математики вообще, в первую очередь с такими, как теория вероятностей, теория гармонических функций, теории конформных отображений, граничных задач аналитических функций, потенциала, распределения значений, римановых поверхностей, субгармонических функций, функциональных алгебр. Через граничные задачи теория Г. с. а. ф. тесно связана с различными областями применения математики.
В связи с тем, что изучение Г. с. а. ф. связано прежде всего с геометрией границы Г области определения Dаналитич. функции  одного комплексного переменного z, в теории Г. с. а. ф. выделились три основных направления.
одного комплексного переменного z, в теории Г. с. а. ф. выделились три основных направления.
а) Изучение поведения  в окрестности изолированной граничной точки
в окрестности изолированной граничной точки  . Наибольшее значение имеет случай существенно особой точки а, к к-рому относятся Сохоцкого теорема, Пикара теорема, Жюлиа теорема, Иверсена теорема.
. Наибольшее значение имеет случай существенно особой точки а, к к-рому относятся Сохоцкого теорема, Пикара теорема, Жюлиа теорема, Иверсена теорема.
б) Изучение поведения  в том случае, когда граница Г есть всюду разрывное множество. Большое значение здесь имела диссертация В. В. Голубева "Однозначные аналитические функции с совершенным множеством особых точек" (1916, см. [1]).
в том случае, когда граница Г есть всюду разрывное множество. Большое значение здесь имела диссертация В. В. Голубева "Однозначные аналитические функции с совершенным множеством особых точек" (1916, см. [1]).
в) Изучение поведения  в том случае, когда область Dограничена непрерывной замкнутой кривой Г. В частности, наиболее важен случай единичного круга.
в том случае, когда область Dограничена непрерывной замкнутой кривой Г. В частности, наиболее важен случай единичного круга.
Случаи а) и в) - в нек-ром смысле крайние, случай б) - промежуточный. Наибольшее внимание исследователей привлек случай в), о к-ром говорится ниже.
Пусть аналитич. функция  определена в конечной односвязной области Dкомплексной плоскости z, ограниченной жордановой спрямляемой кривой Г. Основными проблемами, характерными для классич. направления изучения Г. с. а. ф., являются следующие.
определена в конечной односвязной области Dкомплексной плоскости z, ограниченной жордановой спрямляемой кривой Г. Основными проблемами, характерными для классич. направления изучения Г. с. а. ф., являются следующие.
1) Проблема существования граничных значений, т. е. вопрос о том, при каких условиях и в каком смысле существуют граничные значения 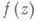 при приближении точки z к Г.
при приближении точки z к Г.
Эта проблема, как и последующие, иначе может быть сформулирована как задача о выделении достаточно обширных классов аналитич. функций в D, имеющих в том или ином смысле граничные значения на достаточно массивных множествах точек Г.
2) Проблем а граничного представления  , т. е. вопрос о том, при каких условиях и при помощи какого аналитич. аппарата может быть выражена зависимость функции
, т. е. вопрос о том, при каких условиях и при помощи какого аналитич. аппарата может быть выражена зависимость функции  от ее граничных значений на Г. Здесь, очевидно, для различных классов аналитич. функций аналитич. аппарат будет варьироваться.
от ее граничных значений на Г. Здесь, очевидно, для различных классов аналитич. функций аналитич. аппарат будет варьироваться.
3) Проблема единственности, или вопрос о том, какими свойствами должно обладать множество  , чтобы две аналитич. функции того или иного класса совпадали всюду в D, если их граничные значения на Есовпадают.
, чтобы две аналитич. функции того или иного класса совпадали всюду в D, если их граничные значения на Есовпадают.
Первым результатом в решении проблемы существования явилась теорема Фату (1906): если аналитич. функция 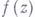 ограничена в единичном круге
ограничена в единичном круге
 то почти всюду по мере Лебега на единичной окружности
то почти всюду по мере Лебега на единичной окружности  существуют радиальные граничные, или предельные, значения
существуют радиальные граничные, или предельные, значения

При высказанных условиях можно показать, что почти всюду на Г существуют не только радиальные, но и угловые граничные значения, или граничные значения по всем некасательным путям. Это означает, что  почти для всех точек
почти для всех точек  стремится к определенному пределу
стремится к определенному пределу  , когда
, когда  стремится к точке
стремится к точке  , оставаясь внутри любого фиксированного угла
, оставаясь внутри любого фиксированного угла

раствора  , меньшего
, меньшего 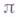 , с вершиной в точке
, с вершиной в точке  > биссектрисой к-рого служит радиус, проведенный в точку
> биссектрисой к-рого служит радиус, проведенный в точку  . В определенном смысле теорема Фату неулучшаема; как показал Н. Н. Лузин (1919), для любого множества
. В определенном смысле теорема Фату неулучшаема; как показал Н. Н. Лузин (1919), для любого множества  меры нуль на Г существует ограниченная аналитич. функция
меры нуль на Г существует ограниченная аналитич. функция  такая, что
такая, что  не имеет радиальных пределов на Е.
не имеет радиальных пределов на Е.
Класс ограниченных аналитич. функций в области Dобозначается  или
или  . После результатов Фату первоочередной задачей выглядело распространение его теорем на более широкие классы функций. Различают следующие основные классы аналитич. функций в единичном круге D, связанные строгими включениями:
. После результатов Фату первоочередной задачей выглядело распространение его теорем на более широкие классы функций. Различают следующие основные классы аналитич. функций в единичном круге D, связанные строгими включениями:

Класс  - это класс однозначных аналитических в Dи непрерывных в замкнутой области
- это класс однозначных аналитических в Dи непрерывных в замкнутой области  функций.
функций.
Классы  для всех положительных чисел р определяются условием
для всех положительных чисел р определяются условием

Для любых  имеют место строгие включения
имеют место строгие включения  Классы
Классы  впервые встречаются у Г. Харди (1915), и их часто наз. классами Харди. При
впервые встречаются у Г. Харди (1915), и их часто наз. классами Харди. При  в
в  можно ввести норму по формуле (2), а в
можно ввести норму по формуле (2), а в  - по формуле
- по формуле

и при этом классы  наделенные, кроме того, естественной структурой векторного пространства, превращаются в банаховы пространства Xарди. При
наделенные, кроме того, естественной структурой векторного пространства, превращаются в банаховы пространства Xарди. При  на
на  можно только ввести метрику
можно только ввести метрику  превращающую
превращающую  в полное метрическое ненормируемое пространство. Класс ограниченных аналитич. функций
в полное метрическое ненормируемое пространство. Класс ограниченных аналитич. функций  содержится в любом классе
содержится в любом классе  .
.
Класс  мероморфных функций
мероморфных функций  в единичном круге Dназ. классом функций ограниченного вида; он был введен Р. Неванлинной в 1924. Класс
в единичном круге Dназ. классом функций ограниченного вида; он был введен Р. Неванлинной в 1924. Класс  можно охарактеризовать как совокупность всех мероморфных функций
можно охарактеризовать как совокупность всех мероморфных функций  в
в  , пред-ставимых в виде отношения двух ограниченных регулярных функций
, пред-ставимых в виде отношения двух ограниченных регулярных функций 
Все регулярные функции  образуют подкласс
образуют подкласс  , причем
, причем  тогда и только тогда, когда выполняется условие
тогда и только тогда, когда выполняется условие

где  при
при  и
и  при
при  В классе
В классе  содержатся все классы
содержатся все классы  .
.
Классы 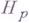 имеют следующее обобщение. Пусть
имеют следующее обобщение. Пусть  - сильно выпуклая функция при
- сильно выпуклая функция при  , т. е. неотрицательная выпуклая неубывающая функция такая, что
, т. е. неотрицательная выпуклая неубывающая функция такая, что  при
при  . Тогда класс
. Тогда класс  определяется условием
определяется условием

[ср. с условием (2), где  ].
].
Основной результат по проблеме существования граничных значений для случая единичного круга Dгласит: каждая мероморфная функция  ограниченного вида в Dпочти всюду на Г имеет угловые граничные значения
ограниченного вида в Dпочти всюду на Г имеет угловые граничные значения 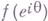 ; эти граничные значения таковы, что функция
; эти граничные значения таковы, что функция  суммируема по Лебегу на Г. Для классов
суммируема по Лебегу на Г. Для классов  ,
,  , или
, или  сюда добавляется свойство: функция
сюда добавляется свойство: функция  или, соответственно,
или, соответственно,  суммируема по Лебегу на Г. Для ограниченных функций
суммируема по Лебегу на Г. Для ограниченных функций  ,
,  , вместо этого имеем
, вместо этого имеем  Таким образом, условие (3) можно охарактеризовать как наиболее широкое достаточное условие на средний рост аналитич. функции
Таким образом, условие (3) можно охарактеризовать как наиболее широкое достаточное условие на средний рост аналитич. функции  при
при  , обеспечивающее существование почти всюду на Г угловых граничных значений.
, обеспечивающее существование почти всюду на Г угловых граничных значений.
Было доказано, что условие (3) нельзя существенно ослабить. Напр., А. Зигмунд (A. Zygmund) доказал, что для произвольной возрастающей функции  ,
,  при
при  существует аналитическая в Dфункция
существует аналитическая в Dфункция  такая, что
такая, что
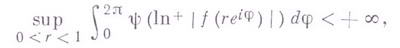
но не имеющая нигде на Г граничных значений. Также и при произвольно медленном росте максимума 
 существуют аналитич. функции без радиальных граничных значений.
существуют аналитич. функции без радиальных граничных значений.
Граничное представление функций  класса
класса  , характеризующее функции этого класса, имеет вид:
, характеризующее функции этого класса, имеет вид:

где  -целое число,
-целое число, , если точка
, если точка  -нуль кратности
-нуль кратности  , и
, и  , если
, если  -полюс кратности
-полюс кратности  - действительное число;
- действительное число;
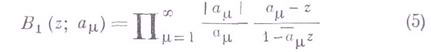
- Бляшке произведение, составленное по всем нулям  функции
функции  внутри Dс учетом их кратности;
внутри Dс учетом их кратности;  - произведение Бляшке вида (5), составленное по всем полюсам
- произведение Бляшке вида (5), составленное по всем полюсам  функции
функции  в D;
в D; - сингулярная функция ограниченной вариации на
- сингулярная функция ограниченной вариации на  с производной, равной нулю почти всюду. Последний интеграл в (4) - типа Лебега - Стилтьеса, первый - типа Лебега.
с производной, равной нулю почти всюду. Последний интеграл в (4) - типа Лебега - Стилтьеса, первый - типа Лебега.
Как показал М. М. Джрбашян (см. [10]), теория мероморфных функций ограниченного вида допускает существенное расширение. Именно, можно ввести семейство классов мероморфных функций  , зависящее от непрерывного параметра
, зависящее от непрерывного параметра  причем классы
причем классы  характеризуются такими пара-метрич. представлениями, из к-рых при
характеризуются такими пара-метрич. представлениями, из к-рых при  получается представление (4). При возрастании
получается представление (4). При возрастании  классы
классы  расширяются, и класс
расширяются, и класс  совпадает с классом Неванлинны N.
совпадает с классом Неванлинны N.
Для аналитич. функций  в представлении (4) следует положить
в представлении (4) следует положить  . Для функций
. Для функций  или
или  в представлении (4) имеем:
в представлении (4) имеем:  есть невозрастающая функция указанного типа. См. также Коши интеграл.
есть невозрастающая функция указанного типа. См. также Коши интеграл.
В проблеме единственности первый результат был получен братьями Ф. и М. Рис (1916): если функция  на множестве
на множестве  положительной меры Лебега на Г имеет радиальные граничные значения
положительной меры Лебега на Г имеет радиальные граничные значения  то
то 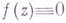 в
в  . Представление (4) позволяет распространить эту теорему на мероморфные ограниченного вида функции. В то же время Н. Н. Лузин построил (1919) для любого множества
. Представление (4) позволяет распространить эту теорему на мероморфные ограниченного вида функции. В то же время Н. Н. Лузин построил (1919) для любого множества  меры нуль аналитич. функцию
меры нуль аналитич. функцию  такую, что
такую, что  всюду на Е, когда
всюду на Е, когда  любым способом, но
любым способом, но 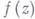 не равна тождественно нулю. Наиболее глубокие и общие граничные теоремы единственности для мероморфных функций общего вида были получены Н. Н. Лузиным и И. И. Приваловым в 1925 (см. Единственности свойства, Лузина - Привалова теоремы).
не равна тождественно нулю. Наиболее глубокие и общие граничные теоремы единственности для мероморфных функций общего вида были получены Н. Н. Лузиным и И. И. Приваловым в 1925 (см. Единственности свойства, Лузина - Привалова теоремы).
Рассмотрим случай произвольной плоской области D, ограничившись, однако, для краткости, одпосвязными областями Dсо спрямляемой границей Г. Условия (2), (3) и (2') равносильны требованию, чтобы субгармонич. функции  и
и  , соответственно, имели гармоническую мажоранту в D. В такой форме эти условия вполне пригодны и естественны для определения классов
, соответственно, имели гармоническую мажоранту в D. В такой форме эти условия вполне пригодны и естественны для определения классов  и
и 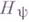 в произвольных областях. Известно, что спрямляемая кривая Г почти во всех точках имеет определенную касательную и нормаль. Включения (1) остаются в силе, равно как и теорема Фату о существовании почти всюду на Г угловых граничных значений для класса
в произвольных областях. Известно, что спрямляемая кривая Г почти во всех точках имеет определенную касательную и нормаль. Включения (1) остаются в силе, равно как и теорема Фату о существовании почти всюду на Г угловых граничных значений для класса  . При этом биссектрисой угловых областей
. При этом биссектрисой угловых областей  следует считать нормаль к Г в точке
следует считать нормаль к Г в точке  . Переносится также теорема единственности Ф. и М. Рисов для класса
. Переносится также теорема единственности Ф. и М. Рисов для класса 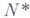 .
.
В случае произвольной области DВ. И. Смирнов ввел также часто употребляемые классы  со следующим определением:
со следующим определением:  если существует последовательность контуров
если существует последовательность контуров  такая, что
такая, что

Классы  особенно удобны при изучении вопросов представимости функций интегралом Коши.
особенно удобны при изучении вопросов представимости функций интегралом Коши.
Значительный интерес вызывает изучение Г. с. а. ф., осуществляющих конформное отображение. Пусть функция  осуществляет конформное отображение единичного круга
осуществляет конформное отображение единичного круга  на область Dплоскости z со спрямляемой границей Г. Доказано, напр., что при этом производная
на область Dплоскости z со спрямляемой границей Г. Доказано, напр., что при этом производная  принадлежит классу Харди
принадлежит классу Харди  в круге
в круге  , а следовательно, она представима в форме (4) с
, а следовательно, она представима в форме (4) с  и невозрастающей сингулярной функцией
и невозрастающей сингулярной функцией  . В. И. Смирнов указал на важность класса Sтаких областей D, для к-рых эта сингулярная функция
. В. И. Смирнов указал на важность класса Sтаких областей D, для к-рых эта сингулярная функция  .В 1937 М. В. Келдыш и М. А. Лаврентьев построили пример области со спрямляемой границей, не входящей в этот класс S Смирнова, что еще более подчеркивает важность характеризации областей типа Смирнова.
.В 1937 М. В. Келдыш и М. А. Лаврентьев построили пример области со спрямляемой границей, не входящей в этот класс S Смирнова, что еще более подчеркивает важность характеризации областей типа Смирнова.
Усилия многих исследователей направлены также на изучение Г. с. а. ф.  многих комплексных переменных
многих комплексных переменных  . Пусть D=Un={
. Пусть D=Un={ |
|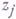 |<1, j=1, 2, ..., n} - единичный поликруг,
|<1, j=1, 2, ..., n} - единичный поликруг,
 - его остов. Класс
- его остов. Класс  аналитич. функций
аналитич. функций  в
в 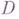 можно определить условием:
можно определить условием:

аналогичным (3), а классы  или
или  - условием типа (
- условием типа ( для случая
для случая  ):
):

где т п- нормированная Хаара мера на  Включения типа
Включения типа  сохраняются. Ана-литпч. функции
сохраняются. Ана-литпч. функции  почти всюду на
почти всюду на  по мере Хаара
по мере Хаара  имеют "радиальные" граничные значения
имеют "радиальные" граничные значения  причем
причем  суммируем на
суммируем на  по мере
по мере  . Для граничных представлений и свойств единственности функций
. Для граничных представлений и свойств единственности функций  в
в  при
при  достаточно простых и общих адекватных характеристик пока (1977) не найдено.
достаточно простых и общих адекватных характеристик пока (1977) не найдено.
Многие граничные свойства переносятся на различные обобщения аналитич. функций, в частности на абстрактные аналитич. функции 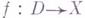 со значениями, напр., в отделимом локально выпуклом топологич. пространстве Xнад полем С.
со значениями, напр., в отделимом локально выпуклом топологич. пространстве Xнад полем С.
Лит.:[1] Голубев В. В., Однозначные аналитические функции. Автоморфные функции, М., 1961; [2] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [3] Привалов И. И., Граничные свойства аналитических функций, 2 изд., М.-Л., 1950; [4] Xавинсон С. Я., в сб.: Итоги науки. Математический анализ. 1963, М., 1965, с. 5-80; [5] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М.-Л., 1941; [6] Носиро К., Предельные множества, пер. с англ., М., 1963; [7] Коллингвуд Э., Ловатер А., Теория предельных множеств, пер. с англ., М., 1971; [8] Мак - Лейн Г., Асимптотические значения голоморфных функций, пер. с англ., М., 1966; [9] Ловатер А., в сб.: Итоги науки и техники. Математический анализ, т. 10, М., 1973, с. 99-259; [10] Джрбашян М. М., Интегральные преобразования и представления функций в комплексной области, М., 1966, гл. 9; [11] Рудин У., Теория функций в поликруге, пер. с англ., М., 1974; [12] Xенкин Г. М., Чирка Е. М., в сб.: Итоги науки и техники. Современные проблемы математики, т. 4, М., 1975, с. 13-142. Е. Д. Соломенцев.

 одного комплексного переменного z, в теории Г. с. а. ф. выделились три основных направления.
одного комплексного переменного z, в теории Г. с. а. ф. выделились три основных направления. в окрестности изолированной граничной точки
в окрестности изолированной граничной точки  . Наибольшее значение имеет случай существенно особой точки а, к к-рому относятся Сохоцкого теорема, Пикара теорема, Жюлиа теорема, Иверсена теорема.
. Наибольшее значение имеет случай существенно особой точки а, к к-рому относятся Сохоцкого теорема, Пикара теорема, Жюлиа теорема, Иверсена теорема. в том случае, когда граница Г есть всюду разрывное множество. Большое значение здесь имела диссертация В. В. Голубева "Однозначные аналитические функции с совершенным множеством особых точек" (1916, см. [1]).
в том случае, когда граница Г есть всюду разрывное множество. Большое значение здесь имела диссертация В. В. Голубева "Однозначные аналитические функции с совершенным множеством особых точек" (1916, см. [1]). в том случае, когда область Dограничена непрерывной замкнутой кривой Г. В частности, наиболее важен случай единичного круга.
в том случае, когда область Dограничена непрерывной замкнутой кривой Г. В частности, наиболее важен случай единичного круга. определена в конечной односвязной области Dкомплексной плоскости z, ограниченной жордановой спрямляемой кривой Г. Основными проблемами, характерными для классич. направления изучения Г. с. а. ф., являются следующие.
определена в конечной односвязной области Dкомплексной плоскости z, ограниченной жордановой спрямляемой кривой Г. Основными проблемами, характерными для классич. направления изучения Г. с. а. ф., являются следующие.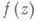 при приближении точки z к Г.
при приближении точки z к Г. , т. е. вопрос о том, при каких условиях и при помощи какого аналитич. аппарата может быть выражена зависимость функции
, т. е. вопрос о том, при каких условиях и при помощи какого аналитич. аппарата может быть выражена зависимость функции  от ее граничных значений на Г. Здесь, очевидно, для различных классов аналитич. функций аналитич. аппарат будет варьироваться.
от ее граничных значений на Г. Здесь, очевидно, для различных классов аналитич. функций аналитич. аппарат будет варьироваться. , чтобы две аналитич. функции того или иного класса совпадали всюду в D, если их граничные значения на Есовпадают.
, чтобы две аналитич. функции того или иного класса совпадали всюду в D, если их граничные значения на Есовпадают.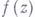 ограничена в единичном круге
ограничена в единичном круге  то почти всюду по мере Лебега на единичной окружности
то почти всюду по мере Лебега на единичной окружности  существуют радиальные граничные, или предельные, значения
существуют радиальные граничные, или предельные, значения 
 почти для всех точек
почти для всех точек  стремится к определенному пределу
стремится к определенному пределу  , когда
, когда  стремится к точке
стремится к точке  , оставаясь внутри любого фиксированного угла
, оставаясь внутри любого фиксированного угла 
 , меньшего
, меньшего 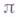 , с вершиной в точке
, с вершиной в точке  > биссектрисой к-рого служит радиус, проведенный в точку
> биссектрисой к-рого служит радиус, проведенный в точку  . В определенном смысле теорема Фату неулучшаема; как показал Н. Н. Лузин (1919), для любого множества
. В определенном смысле теорема Фату неулучшаема; как показал Н. Н. Лузин (1919), для любого множества  меры нуль на Г существует ограниченная аналитич. функция
меры нуль на Г существует ограниченная аналитич. функция  такая, что
такая, что  не имеет радиальных пределов на Е.
не имеет радиальных пределов на Е. или
или  . После результатов Фату первоочередной задачей выглядело распространение его теорем на более широкие классы функций. Различают следующие основные классы аналитич. функций в единичном круге D, связанные строгими включениями:
. После результатов Фату первоочередной задачей выглядело распространение его теорем на более широкие классы функций. Различают следующие основные классы аналитич. функций в единичном круге D, связанные строгими включениями:
 - это класс однозначных аналитических в Dи непрерывных в замкнутой области
- это класс однозначных аналитических в Dи непрерывных в замкнутой области  функций.
функций. для всех положительных чисел р определяются условием
для всех положительных чисел р определяются условием 
 имеют место строгие включения
имеют место строгие включения  Классы
Классы  впервые встречаются у Г. Харди (1915), и их часто наз. классами Харди. При
впервые встречаются у Г. Харди (1915), и их часто наз. классами Харди. При  в
в  можно ввести норму по формуле (2), а в
можно ввести норму по формуле (2), а в  - по формуле
- по формуле 
 наделенные, кроме того, естественной структурой векторного пространства, превращаются в банаховы пространства Xарди. При
наделенные, кроме того, естественной структурой векторного пространства, превращаются в банаховы пространства Xарди. При  на
на  можно только ввести метрику
можно только ввести метрику  превращающую
превращающую  в полное метрическое ненормируемое пространство. Класс ограниченных аналитич. функций
в полное метрическое ненормируемое пространство. Класс ограниченных аналитич. функций  содержится в любом классе
содержится в любом классе  .
. мероморфных функций
мероморфных функций  в единичном круге Dназ. классом функций ограниченного вида; он был введен Р. Неванлинной в 1924. Класс
в единичном круге Dназ. классом функций ограниченного вида; он был введен Р. Неванлинной в 1924. Класс  можно охарактеризовать как совокупность всех мероморфных функций
можно охарактеризовать как совокупность всех мероморфных функций  в
в  , пред-ставимых в виде отношения двух ограниченных регулярных функций
, пред-ставимых в виде отношения двух ограниченных регулярных функций 
 образуют подкласс
образуют подкласс  , причем
, причем  тогда и только тогда, когда выполняется условие
тогда и только тогда, когда выполняется условие 
 при
при  и
и  при
при  В классе
В классе  содержатся все классы
содержатся все классы  .
.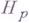 имеют следующее обобщение. Пусть
имеют следующее обобщение. Пусть  - сильно выпуклая функция при
- сильно выпуклая функция при  , т. е. неотрицательная выпуклая неубывающая функция такая, что
, т. е. неотрицательная выпуклая неубывающая функция такая, что  при
при  . Тогда класс
. Тогда класс  определяется условием
определяется условием 
 ].
]. ограниченного вида в Dпочти всюду на Г имеет угловые граничные значения
ограниченного вида в Dпочти всюду на Г имеет угловые граничные значения 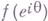 ; эти граничные значения таковы, что функция
; эти граничные значения таковы, что функция  суммируема по Лебегу на Г. Для классов
суммируема по Лебегу на Г. Для классов  ,
,  , или
, или  сюда добавляется свойство: функция
сюда добавляется свойство: функция  или, соответственно,
или, соответственно,  суммируема по Лебегу на Г. Для ограниченных функций
суммируема по Лебегу на Г. Для ограниченных функций  ,
,  , вместо этого имеем
, вместо этого имеем  Таким образом, условие (3) можно охарактеризовать как наиболее широкое достаточное условие на средний рост аналитич. функции
Таким образом, условие (3) можно охарактеризовать как наиболее широкое достаточное условие на средний рост аналитич. функции  при
при  , обеспечивающее существование почти всюду на Г угловых граничных значений.
, обеспечивающее существование почти всюду на Г угловых граничных значений. ,
,  при
при  существует аналитическая в Dфункция
существует аналитическая в Dфункция  такая, что
такая, что 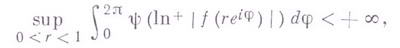

 существуют аналитич. функции без радиальных граничных значений.
существуют аналитич. функции без радиальных граничных значений. класса
класса  , характеризующее функции этого класса, имеет вид:
, характеризующее функции этого класса, имеет вид:
 -целое число,
-целое число, , если точка
, если точка  -нуль кратности
-нуль кратности  , и
, и  , если
, если  -полюс кратности
-полюс кратности  - действительное число;
- действительное число;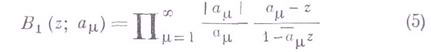
 функции
функции  внутри Dс учетом их кратности;
внутри Dс учетом их кратности;  - произведение Бляшке вида (5), составленное по всем полюсам
- произведение Бляшке вида (5), составленное по всем полюсам  функции
функции  в D;
в D; - сингулярная функция ограниченной вариации на
- сингулярная функция ограниченной вариации на  с производной, равной нулю почти всюду. Последний интеграл в (4) - типа Лебега - Стилтьеса, первый - типа Лебега.
с производной, равной нулю почти всюду. Последний интеграл в (4) - типа Лебега - Стилтьеса, первый - типа Лебега. , зависящее от непрерывного параметра
, зависящее от непрерывного параметра  причем классы
причем классы  характеризуются такими пара-метрич. представлениями, из к-рых при
характеризуются такими пара-метрич. представлениями, из к-рых при  получается представление (4). При возрастании
получается представление (4). При возрастании  классы
классы  расширяются, и класс
расширяются, и класс  совпадает с классом Неванлинны N.
совпадает с классом Неванлинны N. в представлении (4) следует положить
в представлении (4) следует положить  . Для функций
. Для функций  или
или  в представлении (4) имеем:
в представлении (4) имеем:  есть невозрастающая функция указанного типа. См. также Коши интеграл.
есть невозрастающая функция указанного типа. См. также Коши интеграл. на множестве
на множестве  положительной меры Лебега на Г имеет радиальные граничные значения
положительной меры Лебега на Г имеет радиальные граничные значения  то
то 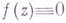 в
в  . Представление (4) позволяет распространить эту теорему на мероморфные ограниченного вида функции. В то же время Н. Н. Лузин построил (1919) для любого множества
. Представление (4) позволяет распространить эту теорему на мероморфные ограниченного вида функции. В то же время Н. Н. Лузин построил (1919) для любого множества  меры нуль аналитич. функцию
меры нуль аналитич. функцию  такую, что
такую, что  всюду на Е, когда
всюду на Е, когда  любым способом, но
любым способом, но 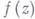 не равна тождественно нулю. Наиболее глубокие и общие граничные теоремы единственности для мероморфных функций общего вида были получены Н. Н. Лузиным и И. И. Приваловым в 1925 (см. Единственности свойства, Лузина - Привалова теоремы).
не равна тождественно нулю. Наиболее глубокие и общие граничные теоремы единственности для мероморфных функций общего вида были получены Н. Н. Лузиным и И. И. Приваловым в 1925 (см. Единственности свойства, Лузина - Привалова теоремы). и
и  , соответственно, имели гармоническую мажоранту в D. В такой форме эти условия вполне пригодны и естественны для определения классов
, соответственно, имели гармоническую мажоранту в D. В такой форме эти условия вполне пригодны и естественны для определения классов  и
и 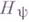 в произвольных областях. Известно, что спрямляемая кривая Г почти во всех точках имеет определенную касательную и нормаль. Включения (1) остаются в силе, равно как и теорема Фату о существовании почти всюду на Г угловых граничных значений для класса
в произвольных областях. Известно, что спрямляемая кривая Г почти во всех точках имеет определенную касательную и нормаль. Включения (1) остаются в силе, равно как и теорема Фату о существовании почти всюду на Г угловых граничных значений для класса  . При этом биссектрисой угловых областей
. При этом биссектрисой угловых областей  следует считать нормаль к Г в точке
следует считать нормаль к Г в точке  . Переносится также теорема единственности Ф. и М. Рисов для класса
. Переносится также теорема единственности Ф. и М. Рисов для класса 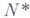 .
. со следующим определением:
со следующим определением:  если существует последовательность контуров
если существует последовательность контуров  такая, что
такая, что 
 особенно удобны при изучении вопросов представимости функций интегралом Коши.
особенно удобны при изучении вопросов представимости функций интегралом Коши. осуществляет конформное отображение единичного круга
осуществляет конформное отображение единичного круга  на область Dплоскости z со спрямляемой границей Г. Доказано, напр., что при этом производная
на область Dплоскости z со спрямляемой границей Г. Доказано, напр., что при этом производная  принадлежит классу Харди
принадлежит классу Харди  в круге
в круге  , а следовательно, она представима в форме (4) с
, а следовательно, она представима в форме (4) с  и невозрастающей сингулярной функцией
и невозрастающей сингулярной функцией  . В. И. Смирнов указал на важность класса Sтаких областей D, для к-рых эта сингулярная функция
. В. И. Смирнов указал на важность класса Sтаких областей D, для к-рых эта сингулярная функция  .В 1937 М. В. Келдыш и М. А. Лаврентьев построили пример области со спрямляемой границей, не входящей в этот класс S Смирнова, что еще более подчеркивает важность характеризации областей типа Смирнова.
.В 1937 М. В. Келдыш и М. А. Лаврентьев построили пример области со спрямляемой границей, не входящей в этот класс S Смирнова, что еще более подчеркивает важность характеризации областей типа Смирнова. многих комплексных переменных
многих комплексных переменных  . Пусть D=Un={
. Пусть D=Un={ |
|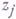 |<1, j=1, 2, ..., n} - единичный поликруг,
|<1, j=1, 2, ..., n} - единичный поликруг,
 - его остов. Класс
- его остов. Класс  аналитич. функций
аналитич. функций  в
в 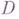 можно определить условием:
можно определить условием:
 или
или  - условием типа (
- условием типа ( для случая
для случая  ):
):
 Включения типа
Включения типа  сохраняются. Ана-литпч. функции
сохраняются. Ана-литпч. функции  почти всюду на
почти всюду на  по мере Хаара
по мере Хаара  имеют "радиальные" граничные значения
имеют "радиальные" граничные значения  причем
причем  суммируем на
суммируем на  по мере
по мере  . Для граничных представлений и свойств единственности функций
. Для граничных представлений и свойств единственности функций  в
в  при
при  достаточно простых и общих адекватных характеристик пока (1977) не найдено.
достаточно простых и общих адекватных характеристик пока (1977) не найдено.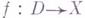 со значениями, напр., в отделимом локально выпуклом топологич. пространстве Xнад полем С.
со значениями, напр., в отделимом локально выпуклом топологич. пространстве Xнад полем С.