|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРАНИЧНЫЕ ЗАДАЧИ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙЗначение ГРАНИЧНЫЕ ЗАДАЧИ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ в математической энциклопедии: - задачи нахождения аналитической в нек-рой области функции по заданному соотношению между граничными значениями ее действительной и мнимой частей. Впервые такая задача была поставлена в 1857 Б. Риманом (см. [1]). Д. Гильберт [2] исследовал граничную задачу в следующей постановке (задача Р и мана- Гильберта): найти функцию где Задача (1) может быть сведена к последовательному решению двух задач Дирихле. Полное исследование задачи, проведенное таким способом, имеется в [3]. Близкой к задаче (1) является задача, к к-рой пришел А. Пуанкаре [4] при разработке математич. теории приливов. Задача Пуанкаре состоит в определении гармонической в области где где в к-рой причем Частным случаем задачи Р.- Г.- П. при Задача Р.- Г.- П. была поставлена и в предположении, что В теории граничных задач важную роль играет понятие индекса задачи - целого числа, определяемого формулой Задача Р.- Г.- П. редуцируется к сингулярному интегральному уравнению вида где функции Пусть Числа Особый интерес представляет тот случай, когда задача разрешима при всякой правой части
в обоих случаях В случае задачи Римана - Гильберта имеют место следующие утверждения: 1) при где Задача Римана - Гильберта тесно связана с так наз. задачей линейного сопряжения. Если L - простая гладкая или кусочно гладкая линия, состоящая из замкнутых контуров, ограничивающих нек-рую область Функцию В задаче линейного сопряжения требуется определить кусочно аналитич. функцию где наз. индексом задачи линейного сопряжения. Когда наз. суммарным индексом задачи линейного сопряжения. Понятия индекса и суммарного индекса играют важную роль в теории задачи линейного сопряжения (см. [5], [6], [7], [8]). На базе теории задачи линейного сопряжения построена теория одномерных сингулярных интегральных уравнений вида (5). Лит.:[1] Риман Б., Сочинения, пер. с нем., М.-Л., 1948; [2] Hilbert D., Grundzuge einer altgemeinen Theorie der linearen Integralgleiehungen, Lpz.-В., 1912; [3] Векуа И. <Н., "Тр. Тбил. матем. ин-та АН Груз. ССР", 1942, т. 11, с. 109-39; [4] Роinсаre Н., Lemons de mecanique celeste, t. 3, P., 1910, ch. 10; [5] Мусхелишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968; [6] Векуа Н. П., Системы сингулярных интегральных уравнений и некоторые граничные задачи, 2 изд., М., 1970; [7] Гахов Ф. Д., Краевые задачи, 2 изд., М., 1963; [8] Xведелидзе Б. В., "Тр. Тбил. матем. ин-та АН Груз. ССР", 1956, т. 23, с. 3-158. А. В. Бицадзе. |
|
|
|

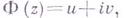 аналитическую в односвязной области
аналитическую в односвязной области  с контуром
с контуром 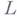 , непрерывную в
, непрерывную в  по граничному условию
по граничному условию 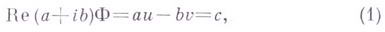
 - заданные на Lдействительные непрерывные функции. Первоначально Д. Гильберт привел эту задачу к сингулярному интегральному уравнению с целью дать пример приложения такого уравнения.
- заданные на Lдействительные непрерывные функции. Первоначально Д. Гильберт привел эту задачу к сингулярному интегральному уравнению с целью дать пример приложения такого уравнения. функции
функции 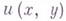 по условию на границе Lэтой области:
по условию на границе Lэтой области:
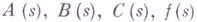 - заданные на Lдействительные функции, s- дуговая абсцисса, п- нормаль к L. Под обобщенной задачей Римана - Гильберта - Пуанкаре (задача Р.-Г.-П.) понимается следующая линейная граничная задача: найти функцию
- заданные на Lдействительные функции, s- дуговая абсцисса, п- нормаль к L. Под обобщенной задачей Римана - Гильберта - Пуанкаре (задача Р.-Г.-П.) понимается следующая линейная граничная задача: найти функцию  , аналитическую в
, аналитическую в 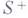 , по граничному условию
, по граничному условию 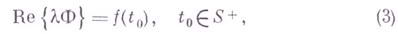
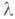 - интегро-дифференциальный оператор, определяемый формулой
- интегро-дифференциальный оператор, определяемый формулой 
 - заданные на L, вообще комплексные, функции класса Н(т. е. удовлетворяющие условию Гельдера),
- заданные на L, вообще комплексные, функции класса Н(т. е. удовлетворяющие условию Гельдера),  - заданная действительная функция класса Н,
- заданная действительная функция класса Н,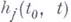 - заданные на L, вообще комплексные, функции вида
- заданные на L, вообще комплексные, функции вида 
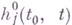 - функции класса Нпо обеим переменным. В правой части (4) под
- функции класса Нпо обеим переменным. В правой части (4) под 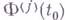 подразумевается граничное значение на Lизнутри области
подразумевается граничное значение на Lизнутри области  производной j-го порядка функции
производной j-го порядка функции  .
. ,
,  является задача Римана - Гильберта; задача Пуанкаре также является частным случаем сформулированной задачи. К задаче Р.- Г.- П. приводятся многие важные граничные задачи, напр, граничные задачи для уравнений с частными производными эллиптич. типа с двумя независимыми переменными.
является задача Римана - Гильберта; задача Пуанкаре также является частным случаем сформулированной задачи. К задаче Р.- Г.- П. приводятся многие важные граничные задачи, напр, граничные задачи для уравнений с частными производными эллиптич. типа с двумя независимыми переменными.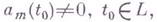 и решена И. Н. Векуа [3].
и решена И. Н. Векуа [3].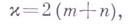 где
где  - приращение
- приращение 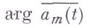 при однократном обходе контура
при однократном обходе контура  в направлении, составляющем область
в направлении, составляющем область  слева.
слева.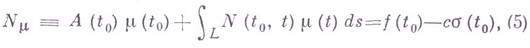
 - искомая действительная функция класса Н, с - искомая действительная постоянная, а
- искомая действительная функция класса Н, с - искомая действительная постоянная, а 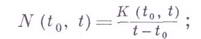
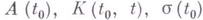 выражаются через
выражаются через 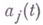 и
и 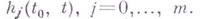
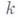 и
и 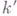 - числа линейно независимых решений соответствующего (5) однородного интегрального уравнения
- числа линейно независимых решений соответствующего (5) однородного интегрального уравнения  и союзного с ним однородного интегрального уравнения
и союзного с ним однородного интегрального уравнения 
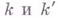 связаны с индексом х задачи Р.- Г.- П. равенством
связаны с индексом х задачи Р.- Г.- П. равенством 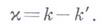
 . Для того чтобы задача Р.- Г.- П. была разрешима при любой правой части
. Для того чтобы задача Р.- Г.- П. была разрешима при любой правой части  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  или
или  , причем в последнем случае решение
, причем в последнем случае решение  уравнения (6) должно удовлетворять условию
уравнения (6) должно удовлетворять условию
 и однородная задача
и однородная задача  имеет ровно
имеет ровно  линейно независимых решений. При
линейно независимых решений. При 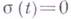 задача Р.- Г.- П. разрешима при любой правой части тогда и только тогда, когда
задача Р.- Г.- П. разрешима при любой правой части тогда и только тогда, когда  .
. неоднородная задача (1) разрешима при любой правой части и 2) при
неоднородная задача (1) разрешима при любой правой части и 2) при  эта задача разрешима тогда и только тогда, когда ,
эта задача разрешима тогда и только тогда, когда ,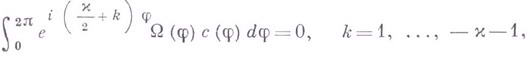

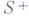 плоскости комплексного переменного
плоскости комплексного переменного 
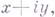 остающуюся слева при обходе L, то дополнение
остающуюся слева при обходе L, то дополнение  до плоскости
до плоскости  обозначается через
обозначается через 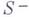 . Пусть функция
. Пусть функция 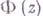 задана и непрерывна в окрестности линии Lвсюду, кроме, быть может, самой L. Говорят, что функция
задана и непрерывна в окрестности линии Lвсюду, кроме, быть может, самой L. Говорят, что функция  непрерывно продолжима на точку
непрерывно продолжима на точку  слева (или справа), если
слева (или справа), если  стремится к определенному пределу
стремится к определенному пределу  [или
[или  ], когда z стремится к г по любому пути, оставаясь слева (или справа) от L.
], когда z стремится к г по любому пути, оставаясь слева (или справа) от L. наз. кусочно аналитической с линией скачка L, если она аналитична в
наз. кусочно аналитической с линией скачка L, если она аналитична в 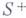 и
и  и непрерывно продолжима на каждую точку
и непрерывно продолжима на каждую точку  как слева так и справа.
как слева так и справа. с линией скачка L, имеющую конечный порядок на бесквнечности, по граничному условию
с линией скачка L, имеющую конечный порядок на бесквнечности, по граничному условию 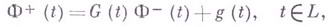
 и
и 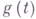 - заданные на
- заданные на 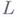 функции класса Н. В предположении, что
функции класса Н. В предположении, что 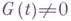 всюду на
всюду на 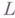 , целое число
, целое число 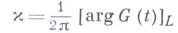
 - кусочно аналитический вектор,
- кусочно аналитический вектор,  - квадратная
- квадратная  -матрица и
-матрица и 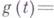
 _ - вектор, причем
_ - вектор, причем 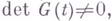 целое число
целое число 