"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРАММАТИКА ПОРОЖДАЮЩАЯ
Значение ГРАММАТИКА ПОРОЖДАЮЩАЯ в математической энциклопедии:
грамматика Хомского,- один из видов формальной грамматики;представляет собой, по существу, частный случай исчисления Поста (см. Поста каноническая система). Систематич. изучение Г. п. было начато в 50-х гг. 20 в. Н. Хомскнм (N. Chomsky), к-рый указал пути ее приложения в лингвистике и выделил наиболее важные для этих приложений классы Г. п.- грамматики составляющих, грамматики бесконтекстные, грамматики автоматные;те же классы оказались особенно интересными и с чисто математич. точки зрения.
Г. п. есть упорядоченная четверка  , где V и W - непересекающиеся конечные множества, наз. соответственно основным и вспомогательным алфавитами, или словарями (их элементы наз. соответственно основными, пли терминальными, и вспомогательными, или нетерминальными, символам и),
, где V и W - непересекающиеся конечные множества, наз. соответственно основным и вспомогательным алфавитами, или словарями (их элементы наз. соответственно основными, пли терминальными, и вспомогательными, или нетерминальными, символам и),  - элемент
- элемент  , наз. начальным символом, и
, наз. начальным символом, и  - конечное множество правил, имеющих вид
- конечное множество правил, имеющих вид  , где
, где  - цепочки ( слова).в алфавите
- цепочки ( слова).в алфавите  и
и  не принадлежит
не принадлежит  ; Rназ. схемой грамматики. Если цепочки
; Rназ. схемой грамматики. Если цепочки  и
и  предста-вимы соответственно в виде
предста-вимы соответственно в виде  где
где  - одно из правил грамматики Г, то говорят, что h непосредственно выводима из
- одно из правил грамматики Г, то говорят, что h непосредственно выводима из  в
в  (обозначение:
(обозначение:  или
или  ). Последовательность цепочек (
). Последовательность цепочек ( ) наз. выводом
) наз. выводом  из
из  в Г, если
в Г, если  ; число песть длина вывода. Вывод наз. полным, если
; число песть длина вывода. Вывод наз. полным, если  и
и  не содержит вспомогательных символов. Если существует вывод цепочки
не содержит вспомогательных символов. Если существует вывод цепочки  из цепочки
из цепочки  в Г, то говорят, что
в Г, то говорят, что  выводима из
выводима из  в Г. Множество цепочек в основном алфавите, выводимых в Г из I, наз. языком, порождаемым грамматикой Г (обозначается через L(Г)). Две Г. п. эквивалентны, если они порождают один и тот же язык. Класс языков, порождаемых всевозможными Г. п., совпадает с классом рекурсивно перечислимых множеств цепочек.
в Г. Множество цепочек в основном алфавите, выводимых в Г из I, наз. языком, порождаемым грамматикой Г (обозначается через L(Г)). Две Г. п. эквивалентны, если они порождают один и тот же язык. Класс языков, порождаемых всевозможными Г. п., совпадает с классом рекурсивно перечислимых множеств цепочек.
Для оценки сложности вывода в Г. п. используются так наз. сигнализирующие функции, важнейшими из к-рых являются временная сложность и емкость. Временная сложность грамматики Г - это функция натурального аргумента  , значение к-рой для каждого правно наименьшему из чисел k, обладающих тем свойством, что для любой цепочки
, значение к-рой для каждого правно наименьшему из чисел k, обладающих тем свойством, что для любой цепочки  такой, что
такой, что  (
( - длина
- длина  ), существует вывод Dэтой цепочки из начального символа Г, длина к-рого не превосходит
), существует вывод Dэтой цепочки из начального символа Г, длина к-рого не превосходит  ; если не существует цепочек хтаких, что
; если не существует цепочек хтаких, что 
Емкость  грамматики Г определяется аналогично с заменой длины вывода
грамматики Г определяется аналогично с заменой длины вывода  наибольшей из длин цепочек
наибольшей из длин цепочек 
Если  - нек-рое множество полных выводов в грамматике Г и
- нек-рое множество полных выводов в грамматике Г и  - множество заключительных цепочек выводов, принадлежащих
- множество заключительных цепочек выводов, принадлежащих  , то
, то  . Если при этом
. Если при этом  задано эффективно, то говорят, что задан нек-рый способ управления выводом в Г. Изучение способов управления выводом существенно для приложений, так как возможность использовать не произвольные, а лишь нек-рые определенные выводы лучше отвечает ситуации, имеющей место в естественном языке. Управление выводом может задаваться, в частности, наложением ограничений на последовательности применяемых в выводе правил (напр., множество таких "допустимых" последовательностей правил может само порождаться нек-рой Г. п. Г'; в этом случае язык определяется упорядоченной парой Г. п.
задано эффективно, то говорят, что задан нек-рый способ управления выводом в Г. Изучение способов управления выводом существенно для приложений, так как возможность использовать не произвольные, а лишь нек-рые определенные выводы лучше отвечает ситуации, имеющей место в естественном языке. Управление выводом может задаваться, в частности, наложением ограничений на последовательности применяемых в выводе правил (напр., множество таких "допустимых" последовательностей правил может само порождаться нек-рой Г. п. Г'; в этом случае язык определяется упорядоченной парой Г. п.  , к-рую наз. обобщенной грамматикой), или на вид входящих в выводы цепочек, или к.-л. более сложным способом (напр., применяемое на очередном шаге правило может зависеть от вида цепочки, полученной на предыдущем шаге).
, к-рую наз. обобщенной грамматикой), или на вид входящих в выводы цепочек, или к.-л. более сложным способом (напр., применяемое на очередном шаге правило может зависеть от вида цепочки, полученной на предыдущем шаге).
При изучении Г. п. естественно возникают алгорит-мич. проблемы. Если 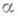 - свойство языков,
- свойство языков,  - нек-рый класс грамматик, и если существует алгоритм, позволяющий по любой грамматике
- нек-рый класс грамматик, и если существует алгоритм, позволяющий по любой грамматике  распознать, обладает ли язык
распознать, обладает ли язык 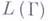 свойством
свойством  , то говорят, что
, то говорят, что  распознаваемо в классе
распознаваемо в классе  В классе всех Г. п. ни одно нетривиальное свойство (т. е. такое, что в соответствующем классе языков есть как языки, обладающие этим свойством, так и не обладающие им) не распознаваемо. Аналогичным образом можно говорить о распознаваемых в нек-ром классе грамматик отношениях. Возникают также проблемы иного типа, напр, о существовании для данной грамматики Г алгоритма, позволяющего по любым п цепочкам
В классе всех Г. п. ни одно нетривиальное свойство (т. е. такое, что в соответствующем классе языков есть как языки, обладающие этим свойством, так и не обладающие им) не распознаваемо. Аналогичным образом можно говорить о распознаваемых в нек-ром классе грамматик отношениях. Возникают также проблемы иного типа, напр, о существовании для данной грамматики Г алгоритма, позволяющего по любым п цепочкам  в ее основном алфавите найти значение заданного предиката
в ее основном алфавите найти значение заданного предиката  для
для  ,
,
 В частности, если
В частности, если  означает
означает  , то речь идет об алгоритме для распознавания принадлежности произвольной цепочки языку
, то речь идет об алгоритме для распознавания принадлежности произвольной цепочки языку  . Если для грамматики Г такой алгоритм есть, существенное значение имеет вопрос о сложности его работы, или, как говорят, о сложности распознавания языка
. Если для грамматики Г такой алгоритм есть, существенное значение имеет вопрос о сложности его работы, или, как говорят, о сложности распознавания языка  .
.
См. также Грамматика составляющих, Грамматика бесконтекстная, Грамматика линейная, Грамматика автоматная, Математическая лингвистика.
Лит.:[1] Гросс М., Лантен А., Теория формальных грамматик, пер. с франц., М., 1971; [2] Гладкий А. В., Формальные грамматики и языки, М., 1973; [3] Норсrоft J. Е., Ullmаn J. D., Formal languages and their relation to automata, Reading (Mass.), 1969; [4] Гладкий А. В., Диковский А. Я., в кн.: Итог" науки и техники. Теория вероятностей. Математическая статистика. Теоретическая кибернетика, 1972, т. 10, с. 107-42; [5] Маслов А. Н., Стоцкий Э. Д., в кн.: Итоги науки и техники. Теория вероятностей. Математическая статистика. Теоретическая кибернетика, 1975, т. 12, с. 155-87; [6] Стоцкий Э. Д., "Проблемы передачи информации", 1971, т. 7, М 1, с. 87-101; № 3, с. 87-102. А. В. Гладкий.

 , где V и W - непересекающиеся конечные множества, наз. соответственно основным и вспомогательным алфавитами, или словарями (их элементы наз. соответственно основными, пли терминальными, и вспомогательными, или нетерминальными, символам и),
, где V и W - непересекающиеся конечные множества, наз. соответственно основным и вспомогательным алфавитами, или словарями (их элементы наз. соответственно основными, пли терминальными, и вспомогательными, или нетерминальными, символам и),  - элемент
- элемент  , наз. начальным символом, и
, наз. начальным символом, и  - конечное множество правил, имеющих вид
- конечное множество правил, имеющих вид  , где
, где  - цепочки ( слова).в алфавите
- цепочки ( слова).в алфавите  и
и  не принадлежит
не принадлежит  ; Rназ. схемой грамматики. Если цепочки
; Rназ. схемой грамматики. Если цепочки  и
и  предста-вимы соответственно в виде
предста-вимы соответственно в виде  где
где  - одно из правил грамматики Г, то говорят, что h непосредственно выводима из
- одно из правил грамматики Г, то говорят, что h непосредственно выводима из  в
в  (обозначение:
(обозначение:  или
или  ). Последовательность цепочек (
). Последовательность цепочек ( ) наз. выводом
) наз. выводом  из
из  в Г, если
в Г, если  ; число песть длина вывода. Вывод наз. полным, если
; число песть длина вывода. Вывод наз. полным, если  и
и  не содержит вспомогательных символов. Если существует вывод цепочки
не содержит вспомогательных символов. Если существует вывод цепочки  из цепочки
из цепочки  в Г, то говорят, что
в Г, то говорят, что  выводима из
выводима из  в Г. Множество цепочек в основном алфавите, выводимых в Г из I, наз. языком, порождаемым грамматикой Г (обозначается через L(Г)). Две Г. п. эквивалентны, если они порождают один и тот же язык. Класс языков, порождаемых всевозможными Г. п., совпадает с классом рекурсивно перечислимых множеств цепочек.
в Г. Множество цепочек в основном алфавите, выводимых в Г из I, наз. языком, порождаемым грамматикой Г (обозначается через L(Г)). Две Г. п. эквивалентны, если они порождают один и тот же язык. Класс языков, порождаемых всевозможными Г. п., совпадает с классом рекурсивно перечислимых множеств цепочек. , значение к-рой для каждого правно наименьшему из чисел k, обладающих тем свойством, что для любой цепочки
, значение к-рой для каждого правно наименьшему из чисел k, обладающих тем свойством, что для любой цепочки  такой, что
такой, что  (
( - длина
- длина  ), существует вывод Dэтой цепочки из начального символа Г, длина к-рого не превосходит
), существует вывод Dэтой цепочки из начального символа Г, длина к-рого не превосходит  ; если не существует цепочек хтаких, что
; если не существует цепочек хтаких, что 
 грамматики Г определяется аналогично с заменой длины вывода
грамматики Г определяется аналогично с заменой длины вывода  наибольшей из длин цепочек
наибольшей из длин цепочек 
 - нек-рое множество полных выводов в грамматике Г и
- нек-рое множество полных выводов в грамматике Г и  - множество заключительных цепочек выводов, принадлежащих
- множество заключительных цепочек выводов, принадлежащих  , то
, то  . Если при этом
. Если при этом  задано эффективно, то говорят, что задан нек-рый способ управления выводом в Г. Изучение способов управления выводом существенно для приложений, так как возможность использовать не произвольные, а лишь нек-рые определенные выводы лучше отвечает ситуации, имеющей место в естественном языке. Управление выводом может задаваться, в частности, наложением ограничений на последовательности применяемых в выводе правил (напр., множество таких "допустимых" последовательностей правил может само порождаться нек-рой Г. п. Г'; в этом случае язык определяется упорядоченной парой Г. п.
задано эффективно, то говорят, что задан нек-рый способ управления выводом в Г. Изучение способов управления выводом существенно для приложений, так как возможность использовать не произвольные, а лишь нек-рые определенные выводы лучше отвечает ситуации, имеющей место в естественном языке. Управление выводом может задаваться, в частности, наложением ограничений на последовательности применяемых в выводе правил (напр., множество таких "допустимых" последовательностей правил может само порождаться нек-рой Г. п. Г'; в этом случае язык определяется упорядоченной парой Г. п.  , к-рую наз. обобщенной грамматикой), или на вид входящих в выводы цепочек, или к.-л. более сложным способом (напр., применяемое на очередном шаге правило может зависеть от вида цепочки, полученной на предыдущем шаге).
, к-рую наз. обобщенной грамматикой), или на вид входящих в выводы цепочек, или к.-л. более сложным способом (напр., применяемое на очередном шаге правило может зависеть от вида цепочки, полученной на предыдущем шаге).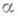 - свойство языков,
- свойство языков,  - нек-рый класс грамматик, и если существует алгоритм, позволяющий по любой грамматике
- нек-рый класс грамматик, и если существует алгоритм, позволяющий по любой грамматике  распознать, обладает ли язык
распознать, обладает ли язык 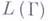 свойством
свойством  , то говорят, что
, то говорят, что  распознаваемо в классе
распознаваемо в классе  В классе всех Г. п. ни одно нетривиальное свойство (т. е. такое, что в соответствующем классе языков есть как языки, обладающие этим свойством, так и не обладающие им) не распознаваемо. Аналогичным образом можно говорить о распознаваемых в нек-ром классе грамматик отношениях. Возникают также проблемы иного типа, напр, о существовании для данной грамматики Г алгоритма, позволяющего по любым п цепочкам
В классе всех Г. п. ни одно нетривиальное свойство (т. е. такое, что в соответствующем классе языков есть как языки, обладающие этим свойством, так и не обладающие им) не распознаваемо. Аналогичным образом можно говорить о распознаваемых в нек-ром классе грамматик отношениях. Возникают также проблемы иного типа, напр, о существовании для данной грамматики Г алгоритма, позволяющего по любым п цепочкам  в ее основном алфавите найти значение заданного предиката
в ее основном алфавите найти значение заданного предиката  для
для  ,
,
 В частности, если
В частности, если  означает
означает  , то речь идет об алгоритме для распознавания принадлежности произвольной цепочки языку
, то речь идет об алгоритме для распознавания принадлежности произвольной цепочки языку  . Если для грамматики Г такой алгоритм есть, существенное значение имеет вопрос о сложности его работы, или, как говорят, о сложности распознавания языка
. Если для грамматики Г такой алгоритм есть, существенное значение имеет вопрос о сложности его работы, или, как говорят, о сложности распознавания языка  .
.