|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛГЕБРАИЧЕСКИЙ МНОГОЧЛЕН НАИЛУЧШЕГО ПРИБЛИЖЕНИЯЗначение АЛГЕБРАИЧЕСКИЙ МНОГОЧЛЕН НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ в математической энциклопедии: - многочлен, наименее уклоняющийся от заданной функции. Точнее, пусть измеримая функция f(x).интегрируема с р-й степенью наз. наилучшим приближением, а многочлен, для к-рого нижняя грань достигается, наз. алгебраическим многочленом наилучшего приближения в Аналогично (*) определяется А. м. н. п. для большого числа тпеременных. Если число переменных m>=2, то А. м. н. п. (в равномерной метрике), вообще говоря, не единствен. Лит.:[1] Чебышев П. Л., Полное собрание сочинений, т. 2, М., 1947, с. 478, с. 152-236; [2] Воrе1 Е., Logons sur les functions de variables reelles et les developpements en serie de polynomes, P., 1905; [3] Jackson D., "Amer. J. Math.", 1924, v.46; [4] Гаркави А. Л., в кн.: Итоги науки. Математический анализ. 1967, М., 1969. Ю. Н. Субботин, |
|
|
|

 на
на  - множество алгебраич. многочленов степени не выше п. Величину
- множество алгебраич. многочленов степени не выше п. Величину 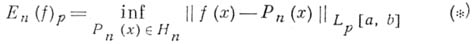
 . Многочлены, наименее уклоняющиеся от данной непрерывной функции в равномерной
. Многочлены, наименее уклоняющиеся от данной непрерывной функции в равномерной  метрике, впервые встретились (1852) у П. Л. Чебышева и были исследованы им в 1856 (см. [1]). Доказательство существования А. м. н. п. дано Э. Борелем [2]. П. Л. Чебышев показал, что
метрике, впервые встретились (1852) у П. Л. Чебышева и были исследованы им в 1856 (см. [1]). Доказательство существования А. м. н. п. дано Э. Борелем [2]. П. Л. Чебышев показал, что 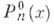 является А. м. н. п. в равномерной метрике тогда и только тогда, когда у разности
является А. м. н. п. в равномерной метрике тогда и только тогда, когда у разности  существует чебышевский алътернанс;в этом случае такой многочлен единствен. При
существует чебышевский алътернанс;в этом случае такой многочлен единствен. При 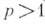 А. м. н. п. единствен в силу строгой выпуклости пространства
А. м. н. п. единствен в силу строгой выпуклости пространства 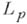 При
При  единственности нет, но для непрерывных функций единственность А. м. н. п. доказана Д. Джексоном {3]). Скорость стремления
единственности нет, но для непрерывных функций единственность А. м. н. п. доказана Д. Джексоном {3]). Скорость стремления 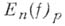 к нулю оценивается в Джексона теореме.
к нулю оценивается в Джексона теореме.