|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРАММАТИКА БЕСКОНТЕКСТНАЯЗначение ГРАММАТИКА БЕСКОНТЕКСТНАЯ в математической энциклопедии: грамматика контекстно-свободная, КС-грамматика,- грамматика составляющих, все правила к-рой имеют вид В определении Г. б. условие непустоты Каждая Г. б. может быть эквивалентным образом приведена к стандартной бинарной форме - Г. б., все правила к-рой имеют вид Если для любой Г. б., порождающей бесконтекстный язык L, и любого натурального Бесконтекстный язык наз. детерминированным, если он допускается нек-рым детерминированным МП-автоматом. Всякий детерминированный язык однозначен, обратное неверно: напр., однозначный язык Сложность вывода. Для любой Г. б. временная сложность н емкость вывода (см. Грамматика порождающая).ограничены сверху и снизу линейными функциями. Поэтому для классификации Г. б. по сложности вывода вводятся нек-рые специфич. характеристики сложности. Эти характеристики разделяются на два типа: одни из них ("древесные") строятся на основе представления вывода в виде дерева (см. Грамматика составляющих), другие ("цепочечные") основаны на учете числа или расположения вхождений вспомогательных символов в промежуточные цепочки вывода; в ряде важных случаев с "древесными" характеристиками можно связать "цепочечные", имеющие тот же порядок роста. Из "древесных" характеристик наиболее тонкую классификацию дает густота, определяемая следующим образом. 1) Каждой вершине Предметом интенсивных исследований является и управление выводом в Г. б. Предложено много различных концепций управления выводом в Г. б. (из к-рых значительная часть переносится и на более широкие классы грамматик). Так, матричная грамматика получается, если задано нек-рое множество конечных последовательностей правил грамматики - "матриц" и допустимыми выводами считаются те, для к-рых последовательности применяемых правил могут быть разбиты на матрицы (т. е. правила применяются только "группами"). В грамматике с порядком на множестве правил задается частичный порядок и на каждом шаге разрешается применять только такие правила, для к-рых никакие предшествующие в смысле этого порядка правила не применимы к полученной к данному моменту цепочке. В программированной грамматике каждому правилу сопоставляются два множества правил - "успешное" и "безуспешное"; применение каждого правила распадается на два этапа: на первом этапе проверяется, входит ли левая часть правила в полученную к данному моменту цепочку; если да, то второй этап состоит в замене левой части правила правой и выборе из "успешного" множества правила для применения на следующем шаге; если нет, то второй этап сводится к выбору из "безуспешного" множества правила для применения на следующем шаге. Класс языков, порождаемых программированными Г. б. без правил с пустой правой частью, является собственным подклассом класса НС-языков и содержит классы языков, порождаемых матричными Г. б. и Г. б. с порядком; в то же время оба эти класса шире класса бесконтекстных языков. При наличии правил с пустой правой частью программированные Г. б. порождают произвольные рекурсивно перечислимые языки. Алгоритмические проблемы. Существуют алгоритмы, позволяющие по любой Г. б. распознавать, является ли порождаемый ею язык пустым, соответственно конечным. В классе Г. б. нераспознаваемы, в частности, следующие свойства языков и отношения между языками: иметь пустое, соответственно конечное или бесконтекстное дополнение; быть однозначным, соответственно детерминированным, линейным или автоматным языком; Сложность распознавания. Принадлежность цепочки языку, порождаемому заданной Г. б., может быть распознана алгоритмом Кока, допускающим реализацию на машине Тьюринга с одной лентой и одной, головкой, время работы к-рой пропорционально четвертой степени длины цепочки; при увеличении числа лент или головок до трех четвертая степень может быть заменена третьей. См. также Грамматика автоматная, Грамматика линейная. Лит.:[1] Гинзбург С., Математическая теория контекстно-свободных языков, пер. с англ., М.. 1970. А. В. Гладкий. |
|
|
|

 где А - вспомогательный символ и
где А - вспомогательный символ и  - непустая цепочка (так наз. бесконтекстные правила). Языки, порождаемые такими грамматиками, наз. бесконтекстными языками. Напр., язык
- непустая цепочка (так наз. бесконтекстные правила). Языки, порождаемые такими грамматиками, наз. бесконтекстными языками. Напр., язык  порождается Г. б. с правилами
порождается Г. б. с правилами  (
( - начальный символ).
- начальный символ). можно отбросить без существенного изменения класса языков (добавляются лишь языки, получаемые из бесконтекстных присоединением пустой цепочки). Г. б.- наиболее употребительный в приложениях класс формальных грамматик;они широко используются для построения математич. моделей естественных языков (см. Математическая лингвистика).и для описания языков программирования. Класс бесконтекстных языков является собственным подклассом класса НС-языков (см. Грамматика составляющих;напр., НС-язык
можно отбросить без существенного изменения класса языков (добавляются лишь языки, получаемые из бесконтекстных присоединением пустой цепочки). Г. б.- наиболее употребительный в приложениях класс формальных грамматик;они широко используются для построения математич. моделей естественных языков (см. Математическая лингвистика).и для описания языков программирования. Класс бесконтекстных языков является собственным подклассом класса НС-языков (см. Грамматика составляющих;напр., НС-язык 
 не бесконтекстный) и совпадает с классом языков, допускаемых так наз. автоматами с магазинной памятью (МП -автоматами).
не бесконтекстный) и совпадает с классом языков, допускаемых так наз. автоматами с магазинной памятью (МП -автоматами).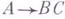 и
и  , а также кнормальной форме Грейбах - Г. б., все правила к-рой имеют вид
, а также кнормальной форме Грейбах - Г. б., все правила к-рой имеют вид  ,
, и
и  (в обоих случаях А, В, С - вспомогательные символы, а - основной символ). Бесконтекстные языки определяются также грамматиками категориальными, грамматиками доминационными, грамматиками зависимостей. Иногда для определения бесконтекстных языков используются так наз. нормальные системы уравнений в языках, представляющие собой другую форму записи Г. б. Класс бесконтекстных языков замкнут относительно объединения, умножения, подстановки и усеченной итерации (а при наличии правил с пустой правой частью и относительно итерации) и не замкнут относительно пересечения и дополнения. Г. б. Г наз. однозначной, если для каждой цепочки языка L(Г)имеется единственное дерево вывода в Г. Бесконтекстный язык наз. однозначным, если он порождается нек-рой однозначной Г. б.; в противном случае он наз. неоднозначным (или существенно неоднозначным, существенно неопределенным). Пример неоднозначного бесконтекстного языка -
(в обоих случаях А, В, С - вспомогательные символы, а - основной символ). Бесконтекстные языки определяются также грамматиками категориальными, грамматиками доминационными, грамматиками зависимостей. Иногда для определения бесконтекстных языков используются так наз. нормальные системы уравнений в языках, представляющие собой другую форму записи Г. б. Класс бесконтекстных языков замкнут относительно объединения, умножения, подстановки и усеченной итерации (а при наличии правил с пустой правой частью и относительно итерации) и не замкнут относительно пересечения и дополнения. Г. б. Г наз. однозначной, если для каждой цепочки языка L(Г)имеется единственное дерево вывода в Г. Бесконтекстный язык наз. однозначным, если он порождается нек-рой однозначной Г. б.; в противном случае он наз. неоднозначным (или существенно неоднозначным, существенно неопределенным). Пример неоднозначного бесконтекстного языка -
 найдется цепочка, имеющая более пдеревьев вывода в данной грамматике, говорят, что Lимеет бесконечную степень неоднозначности; пример - язык
найдется цепочка, имеющая более пдеревьев вывода в данной грамматике, говорят, что Lимеет бесконечную степень неоднозначности; пример - язык 
 где
где  означает обращение (т. е. если
означает обращение (т. е. если  ).
). не является детерминированным.
не является детерминированным. конечного дерева с корнем сопоставляется густота
конечного дерева с корнем сопоставляется густота  - число
- число  такое, что: если
такое, что: если  - концевой узел, то
- концевой узел, то  ; если
; если  - все узлы, в к-рые из
- все узлы, в к-рые из  идут дуги,
идут дуги,  и
и  , то: а) если
, то: а) если  только для одного
только для одного  б) в противном случае
б) в противном случае  . 2) Густота корня дерева наз. густотой дерева. 3) Если Г есть Г. б., ее густота
. 2) Густота корня дерева наз. густотой дерева. 3) Если Г есть Г. б., ее густота  определяется аналогично временной сложности с заменой длины вывода густотой дерева вывода. Одинаковый с густотой порядок роста имеет (для Г. б.) активная емкость
определяется аналогично временной сложности с заменой длины вывода густотой дерева вывода. Одинаковый с густотой порядок роста имеет (для Г. б.) активная емкость  , определяемая аналогично емкости с заменой длины цепочки
, определяемая аналогично емкости с заменой длины цепочки  числом вхождений в wi вспомогательных символов. Густота всякой Г. б. ограничена сверху логарнфмич. функцией. Существуют бесконтекстные языки, для к-рых густоты любых порождающих их Г. б. имеют логарифмич. порядок роста, напр, множество всевозможных "правильных скобочных последовательностей" (т. е. последовательностей левых и правых круглых скобок, расставленных так, как это делается, напр., в арифметич. выражениях). В то же время языки, порождаемые Г. б., густоты к-рых ограничены константами, составляют обширный класс, совпадающий с замыканием класса линейных языков (см. Грамматика линейная).относительно подстановки. Имеются бесконечные последовательности функций, промежуточных по порядку роста между константой и логарифмом, такие, что для любых двух соседних членов последовательности найдется бесконтекстный язык, для к-рого наименьшая по порядку густота порождающей его Г. б. заключена между этими функциями. Употребляются и другие характеристики сложности вывода в Г. б.
числом вхождений в wi вспомогательных символов. Густота всякой Г. б. ограничена сверху логарнфмич. функцией. Существуют бесконтекстные языки, для к-рых густоты любых порождающих их Г. б. имеют логарифмич. порядок роста, напр, множество всевозможных "правильных скобочных последовательностей" (т. е. последовательностей левых и правых круглых скобок, расставленных так, как это делается, напр., в арифметич. выражениях). В то же время языки, порождаемые Г. б., густоты к-рых ограничены константами, составляют обширный класс, совпадающий с замыканием класса линейных языков (см. Грамматика линейная).относительно подстановки. Имеются бесконечные последовательности функций, промежуточных по порядку роста между константой и логарифмом, такие, что для любых двух соседних членов последовательности найдется бесконтекстный язык, для к-рого наименьшая по порядку густота порождающей его Г. б. заключена между этими функциями. Употребляются и другие характеристики сложности вывода в Г. б. Существуют такие Г. б.
Существуют такие Г. б.  , для к-рых нет алгоритмов, позволяющих по произвольным, цепочкам хи у в основном алфавите
, для к-рых нет алгоритмов, позволяющих по произвольным, цепочкам хи у в основном алфавите  грамматики
грамматики  (соответственно в основном алфавите
(соответственно в основном алфавите  грамматика
грамматика  ) распознавать, замещаема ли х на у относительно
) распознавать, замещаема ли х на у относительно  и
и  (соответственно взаимозамещаемы ли хи уотносительно
(соответственно взаимозамещаемы ли хи уотносительно  и
и  ; см. Аналитическая модель языка).
; см. Аналитическая модель языка).