|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРАМА - ШАРЛЬЕ РЯДЗначение ГРАМА - ШАРЛЬЕ РЯД в математической энциклопедии: - ряд, определяемый выражением или где х - нормированное значение случайной величины. Ряд (1) наз. Г.- Ш. р. типа А;здесь где Ряд (2) наз. Г.- Ш. р. типа В;здесь а Ограничиваясь первыми членами ряда (2), получают где принятой для интерполирования между значениями - характеристическая функция биномиального распределения. Разложение Лит.:[1] Gram J. P., "J. reine und angew. Math.", 1883, Bd 94, S. 41-73; [2] Charlier C. V. L., "Arkiv Mat., Astr., Fys.", 1914, b. 2, №25, s. 1 - 17; [3] Mитропольский А. К., Кривые распределения. Л., 1960. А. К. Митрополъский. |
|
|
|




 есть k-я производная от
есть k-я производная от  , к-рую можно представить в виде
, к-рую можно представить в виде 
 - многочлены Чебышева - Эрмита. Производные
- многочлены Чебышева - Эрмита. Производные  и многочлены
и многочлены  обладают свойствами ортогональности, благодаря чему коэффициенты а k можно определить при помощи основных моментов rk данного ряда распределения. Ограничиваясь первыми членами ряда (1), получают
обладают свойствами ортогональности, благодаря чему коэффициенты а k можно определить при помощи основных моментов rk данного ряда распределения. Ограничиваясь первыми членами ряда (1), получают 
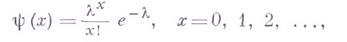
 - многочлены, аналогичные многочленам
- многочлены, аналогичные многочленам 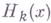 .
.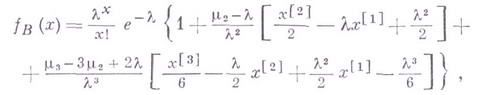
 - центральные моменты распределения, а
- центральные моменты распределения, а 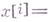
 Г.- Ш. р. были получены Дж. Грамом [1] и К. Шарлье [2] при исследовании функции вида
Г.- Ш. р. были получены Дж. Грамом [1] и К. Шарлье [2] при исследовании функции вида 
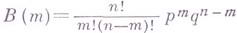 - общего члена биномиального распределения, где
- общего члена биномиального распределения, где 
 по степеням tприводит к Г.- Ш. р. типа Адля
по степеням tприводит к Г.- Ш. р. типа Адля  , а разложение
, а разложение  по степеням рприводит к Г.- Ш. р. типа В.
по степеням рприводит к Г.- Ш. р. типа В.