" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ГОРДИНГА НЕРАВЕНСТВО

Значение ГОРДИНГА НЕРАВЕНСТВО в математической энциклопедии:

неравенство, имеющее вид:

где - комплексная функция с компактным (в G).носителем, - ограниченная область и

- интегральная квадратичная форма с непрерывными в комплексными коэффициентами . Достаточным условием справедливости Г. н. для любой функции 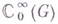является существование такой положительной постоянной , что

для любого и всех действительных векторов . Г. н. сформулировано и доказано Л. Гордингом 11].

Лит.:[1] Garding L., "Math, scand.", 1953, bd. 1, № 1, s. 55-72; [2] Иосида К., Функциональный анализ, пер. с англ., М., 1967. А. А. Дезин.