"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОТОПИЯ
Значение ГОМОТОПИЯ в математической энциклопедии:
гомотопность двух непрерывных отображений  - формализация интуитивного представления о деформи-руемости одного отображения в другое. Точнее, отображения
- формализация интуитивного представления о деформи-руемости одного отображения в другое. Точнее, отображения  паз. гомотопными (обозначение
паз. гомотопными (обозначение 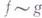 ), если существует такое семейство непрерывных отображений
), если существует такое семейство непрерывных отображений  непрерывно зависящих от параметра
непрерывно зависящих от параметра  что
что  (фиксация отрезка [0, 1] произведена здесь лишь по соображениям технич. удобства; ясно, что вместо него можно взять любой другой отрезок действительной оси). Это семейство (называемое гомотопией связывающей
(фиксация отрезка [0, 1] произведена здесь лишь по соображениям технич. удобства; ясно, что вместо него можно взять любой другой отрезок действительной оси). Это семейство (называемое гомотопией связывающей  ) является путем в пространстве
) является путем в пространстве  всех непрерывных отображений
всех непрерывных отображений  , связывающим точку f с точкой g, так что гомотопность отображений является специализацией на случай пространств отображений общего отношения "быть связанным непрерывным путем". Поэтому, в частности, отношение гомотопности является отношением эквивалентности, а соответствующие классы (они называются гомотопич. классами) представляют собой компоненты линейной связности пространства
, связывающим точку f с точкой g, так что гомотопность отображений является специализацией на случай пространств отображений общего отношения "быть связанным непрерывным путем". Поэтому, в частности, отношение гомотопности является отношением эквивалентности, а соответствующие классы (они называются гомотопич. классами) представляют собой компоненты линейной связности пространства 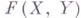 . Для придания сказанному точного смысла необходимо уточнить, что означает выражение "отображения ft непрерывно зависят от t". Самый естественный путь состоит во введении в
. Для придания сказанному точного смысла необходимо уточнить, что означает выражение "отображения ft непрерывно зависят от t". Самый естественный путь состоит во введении в  топологии (или хотя бы псевдотопологии). Однако по традиции принято поступать иначе. Именно, но определению, считается, что
топологии (или хотя бы псевдотопологии). Однако по традиции принято поступать иначе. Именно, но определению, считается, что  непрерывно зависит от t, если функция
непрерывно зависит от t, если функция  непрерывна по совокупности переменных, т. е. если непрерывно отображение
непрерывна по совокупности переменных, т. е. если непрерывно отображение  , определенное формулой
, определенное формулой  (это отображение также часто наз. гомотопией, связывающей
(это отображение также часто наз. гомотопией, связывающей  ).
).
Описанные Г. иногда наз. свободными, чтобы отличить их от "связанных" Г., возникающих, когда фиксирован нек-рый класс  непрерывных отображений
непрерывных отображений  и наложено требование, чтобы
и наложено требование, чтобы  для любого
для любого 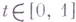 . Напр., если задано подпространство
. Напр., если задано подпространство  , то можно рассматривать связанные на Агомотопий, отличающиеся тем, что
, то можно рассматривать связанные на Агомотопий, отличающиеся тем, что  на Адля всех t. В этом случае говорят, что отображение
на Адля всех t. В этом случае говорят, что отображение  гомотопно отображению
гомотопно отображению  относительно Аи пишут
относительно Аи пишут

Другой тип "связанных" Г. возникает, когда в Xи У выбраны подпространства  и рассматриваются лишь отображения
и рассматриваются лишь отображения  , удовлетворяющие условию
, удовлетворяющие условию  . Такие отображения наз. отображениями пары
. Такие отображения наз. отображениями пары  в пару
в пару  [обозначение
[обозначение  , а соответствующие Г. [т. е. гомотопий, для к-рых
, а соответствующие Г. [т. е. гомотопий, для к-рых  для всех t] - гомотопиями отображений пар. Вместо пар можно рассматривать тройки
для всех t] - гомотопиями отображений пар. Вместо пар можно рассматривать тройки  (с условием
(с условием  или без этого условия), четверки и т. п. Можно рассматривать, напр., Г. отображений пар относительно третьего подпространства и т. д. Возможны и принципиально другие типы "связанных" Г.
или без этого условия), четверки и т. п. Можно рассматривать, напр., Г. отображений пар относительно третьего подпространства и т. д. Возможны и принципиально другие типы "связанных" Г.
Задача установления гомотопичности ("связанной" или нет) двух данных отображений  равносильна задаче распространения на все
равносильна задаче распространения на все  непрерывного отображения в Y, заданного на
непрерывного отображения в Y, заданного на  (а в задаче гомотопности rel A - на
(а в задаче гомотопности rel A - на 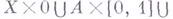
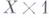 ). В этом смысле задача гомотопности является частным случаем задачи распространения. Вместе с тем в широком классе случаев (а именно, для так наз. корасслоений). возможность распространения на все Xнепрерывного отображения
). В этом смысле задача гомотопности является частным случаем задачи распространения. Вместе с тем в широком классе случаев (а именно, для так наз. корасслоений). возможность распространения на все Xнепрерывного отображения  , заданного на подпространстве
, заданного на подпространстве  , зависит только от его гомотопич. класса. Эта тесная связь задачи гомотопности и задачи распространения обусловливает их совместное рассмотрение в рамках так наз. теории гомотопий. См. Гомотопический тип. м. М. Постников.
, зависит только от его гомотопич. класса. Эта тесная связь задачи гомотопности и задачи распространения обусловливает их совместное рассмотрение в рамках так наз. теории гомотопий. См. Гомотопический тип. м. М. Постников.

 - формализация интуитивного представления о деформи-руемости одного отображения в другое. Точнее, отображения
- формализация интуитивного представления о деформи-руемости одного отображения в другое. Точнее, отображения  паз. гомотопными (обозначение
паз. гомотопными (обозначение 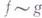 ), если существует такое семейство непрерывных отображений
), если существует такое семейство непрерывных отображений  непрерывно зависящих от параметра
непрерывно зависящих от параметра  что
что  (фиксация отрезка [0, 1] произведена здесь лишь по соображениям технич. удобства; ясно, что вместо него можно взять любой другой отрезок действительной оси). Это семейство (называемое гомотопией связывающей
(фиксация отрезка [0, 1] произведена здесь лишь по соображениям технич. удобства; ясно, что вместо него можно взять любой другой отрезок действительной оси). Это семейство (называемое гомотопией связывающей  ) является путем в пространстве
) является путем в пространстве  всех непрерывных отображений
всех непрерывных отображений  , связывающим точку f с точкой g, так что гомотопность отображений является специализацией на случай пространств отображений общего отношения "быть связанным непрерывным путем". Поэтому, в частности, отношение гомотопности является отношением эквивалентности, а соответствующие классы (они называются гомотопич. классами) представляют собой компоненты линейной связности пространства
, связывающим точку f с точкой g, так что гомотопность отображений является специализацией на случай пространств отображений общего отношения "быть связанным непрерывным путем". Поэтому, в частности, отношение гомотопности является отношением эквивалентности, а соответствующие классы (они называются гомотопич. классами) представляют собой компоненты линейной связности пространства 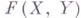 . Для придания сказанному точного смысла необходимо уточнить, что означает выражение "отображения ft непрерывно зависят от t". Самый естественный путь состоит во введении в
. Для придания сказанному точного смысла необходимо уточнить, что означает выражение "отображения ft непрерывно зависят от t". Самый естественный путь состоит во введении в  топологии (или хотя бы псевдотопологии). Однако по традиции принято поступать иначе. Именно, но определению, считается, что
топологии (или хотя бы псевдотопологии). Однако по традиции принято поступать иначе. Именно, но определению, считается, что  непрерывно зависит от t, если функция
непрерывно зависит от t, если функция  непрерывна по совокупности переменных, т. е. если непрерывно отображение
непрерывна по совокупности переменных, т. е. если непрерывно отображение  , определенное формулой
, определенное формулой  (это отображение также часто наз. гомотопией, связывающей
(это отображение также часто наз. гомотопией, связывающей  ).
). непрерывных отображений
непрерывных отображений  и наложено требование, чтобы
и наложено требование, чтобы  для любого
для любого 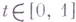 . Напр., если задано подпространство
. Напр., если задано подпространство  , то можно рассматривать связанные на Агомотопий, отличающиеся тем, что
, то можно рассматривать связанные на Агомотопий, отличающиеся тем, что  на Адля всех t. В этом случае говорят, что отображение
на Адля всех t. В этом случае говорят, что отображение  гомотопно отображению
гомотопно отображению  относительно Аи пишут
относительно Аи пишут 
 и рассматриваются лишь отображения
и рассматриваются лишь отображения  , удовлетворяющие условию
, удовлетворяющие условию  . Такие отображения наз. отображениями пары
. Такие отображения наз. отображениями пары  в пару
в пару  [обозначение
[обозначение  , а соответствующие Г. [т. е. гомотопий, для к-рых
, а соответствующие Г. [т. е. гомотопий, для к-рых  для всех t] - гомотопиями отображений пар. Вместо пар можно рассматривать тройки
для всех t] - гомотопиями отображений пар. Вместо пар можно рассматривать тройки  (с условием
(с условием  или без этого условия), четверки и т. п. Можно рассматривать, напр., Г. отображений пар относительно третьего подпространства и т. д. Возможны и принципиально другие типы "связанных" Г.
или без этого условия), четверки и т. п. Можно рассматривать, напр., Г. отображений пар относительно третьего подпространства и т. д. Возможны и принципиально другие типы "связанных" Г. равносильна задаче распространения на все
равносильна задаче распространения на все  непрерывного отображения в Y, заданного на
непрерывного отображения в Y, заданного на  (а в задаче гомотопности rel A - на
(а в задаче гомотопности rel A - на 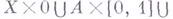
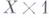 ). В этом смысле задача гомотопности является частным случаем задачи распространения. Вместе с тем в широком классе случаев (а именно, для так наз. корасслоений). возможность распространения на все Xнепрерывного отображения
). В этом смысле задача гомотопности является частным случаем задачи распространения. Вместе с тем в широком классе случаев (а именно, для так наз. корасслоений). возможность распространения на все Xнепрерывного отображения  , заданного на подпространстве
, заданного на подпространстве  , зависит только от его гомотопич. класса. Эта тесная связь задачи гомотопности и задачи распространения обусловливает их совместное рассмотрение в рамках так наз. теории гомотопий. См. Гомотопический тип. м. М. Постников.
, зависит только от его гомотопич. класса. Эта тесная связь задачи гомотопности и задачи распространения обусловливает их совместное рассмотрение в рамках так наз. теории гомотопий. См. Гомотопический тип. м. М. Постников.