"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОТОПИЧЕСКИЙ ТИП
Значение ГОМОТОПИЧЕСКИЙ ТИП в математической энциклопедии:
топологизированной категории - проективная система топологич. пространств, ассоциированная с топологизированной категорией и позволяющая определять гомотопические группы этой категории, группы гомологии и когомологий со значениями в абелевой группе и т. д.
Рассматриваются только локально связные топологизированные категории  , т. е. такие категории С, снабженные топологией Гротендика
, т. е. такие категории С, снабженные топологией Гротендика 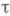 , любой объект к-рых представим в виде копроизведения
, любой объект к-рых представим в виде копроизведения  неразложимых объектов
неразложимых объектов  играет роль множества связных компонент топологич. пространства. Множество индексов I определено однозначно с точностью до биекции; оно обозначается
играет роль множества связных компонент топологич. пространства. Множество индексов I определено однозначно с точностью до биекции; оно обозначается  . Сопоставление
. Сопоставление  определяет функтор из категории Св категорию множеств. Произвольное покрытие
определяет функтор из категории Св категорию множеств. Произвольное покрытие  объекта Xв топологии
объекта Xв топологии  определяет симплициальный объект U. в категории С, для к-рого
определяет симплициальный объект U. в категории С, для к-рого

и симплициальное множество  . Геометрич. реализация симплициального* множества
. Геометрич. реализация симплициального* множества  дает топологич. пространство
дает топологич. пространство  . Для любого измельчения
. Для любого измельчения  - покрытия
- покрытия  (
( пропускается через
пропускается через  ) определено (с точностью до гомотопий) непрерывное отображение
) определено (с точностью до гомотопий) непрерывное отображение  . Таким образом, объекту Xсопоставляется проективная система топологич. пространств
. Таким образом, объекту Xсопоставляется проективная система топологич. пространств  , где
, где  - семейство всех покрытий объекта X.
- семейство всех покрытий объекта X.
Это определение аналогично определению когомологий Чеха; известно, однако, что в общем случае когомологий Чеха дают "правильные" когомологий только в размерностях 0 и 1. Поэтому приведенная выше конструкция не может считаться удовлетворительной. В [1] введено понятие гиперпокрытия, обобщающее симплициальные объекты U., построенные выше для покрытий  . Это - снова симплициальный объект K, в топологизированной категории
. Это - снова симплициальный объект K, в топологизированной категории  с финальным объектом X, удовлетворяющий условиям:
с финальным объектом X, удовлетворяющий условиям:  - покрытие объекта X;для любого пканонич. морфизм
- покрытие объекта X;для любого пканонич. морфизм 
 является покрытием, где
является покрытием, где 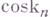 - функтор п- гокоскелета.
- функтор п- гокоскелета.
Сопоставление каждому гиперпокрытию K, топологич. пространства  приводит к проективной системе пространств, параметризованной гиперпокрытиями.
приводит к проективной системе пространств, параметризованной гиперпокрытиями.
Это и определяет гомотопический тип (а точнее - прогомотопический тип) топологизированной категории  с финальным объектом X. Группы гомотопий, гомологии и когомологий вводятся стандартным способом.
с финальным объектом X. Группы гомотопий, гомологии и когомологий вводятся стандартным способом.
Г. т. топологизированной категории, ассоциированной со схемой, позволяет определить Г. т. схемы. Наиболее часто рассматривают случай этальной топологии  на схеме X. В этом случае Г. т. схемы Xпредставляет собой прообъект категории пунктированных симплициальных множеств или категории конечных клеточных комплексов. Определяемые для таких объектов гомотопические группы
на схеме X. В этом случае Г. т. схемы Xпредставляет собой прообъект категории пунктированных симплициальных множеств или категории конечных клеточных комплексов. Определяемые для таких объектов гомотопические группы  являются проконечнымн группами и наз. i-ми гомотопическими группами схемы X(см. [2]). Если X - нормальная схема, то
являются проконечнымн группами и наз. i-ми гомотопическими группами схемы X(см. [2]). Если X - нормальная схема, то  совпадает с фундаментальной группой схемы, определяемой по Гротен-дику [3]. Г. т. точки
совпадает с фундаментальной группой схемы, определяемой по Гротен-дику [3]. Г. т. точки 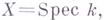 где
где 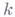 - поле, совпадает с проективным пределом пространств Эйленберга - Маклейна
- поле, совпадает с проективным пределом пространств Эйленберга - Маклейна  где
где  - группа Галуа конечного расширения Галуа
- группа Галуа конечного расширения Галуа  поля
поля 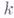 . В случае алгебраич. многообразий над полем комплексных чисел
. В случае алгебраич. многообразий над полем комплексных чисел  имеет место теорема сравнения: группы
имеет место теорема сравнения: группы  являются проконечным пополнением обычных гомотопич. групп
являются проконечным пополнением обычных гомотопич. групп  комплексного пространства Х ап, ассоциированного с X.
комплексного пространства Х ап, ассоциированного с X.
Лит.:[1] Труды международного конгресса математиков (Москва. 1966), М., 1908, с. 44-56; [2] Theorie des Toposes et coliomologie etale des schimas, t. 1-3, B.-Hdlb.-N.Y.,1974; [3] ArtinM., Mazur В., Etale homotopy, B.-Hdlb.- N. Y., 1969; [41 Сулляван Д., Геометрическая топология, пер. с англ., М., 1975; [5] Revetements etales et groupe fondamental (S6A1), В.-Hdlb.-N.Y., 1971.
В. И. Данилов, И. В. Долгачев.

 , т. е. такие категории С, снабженные топологией Гротендика
, т. е. такие категории С, снабженные топологией Гротендика 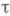 , любой объект к-рых представим в виде копроизведения
, любой объект к-рых представим в виде копроизведения  неразложимых объектов
неразложимых объектов  играет роль множества связных компонент топологич. пространства. Множество индексов I определено однозначно с точностью до биекции; оно обозначается
играет роль множества связных компонент топологич. пространства. Множество индексов I определено однозначно с точностью до биекции; оно обозначается  . Сопоставление
. Сопоставление  определяет функтор из категории Св категорию множеств. Произвольное покрытие
определяет функтор из категории Св категорию множеств. Произвольное покрытие  объекта Xв топологии
объекта Xв топологии  определяет симплициальный объект U. в категории С, для к-рого
определяет симплициальный объект U. в категории С, для к-рого 
 . Геометрич. реализация симплициального* множества
. Геометрич. реализация симплициального* множества  дает топологич. пространство
дает топологич. пространство  . Для любого измельчения
. Для любого измельчения  - покрытия
- покрытия  (
( пропускается через
пропускается через  ) определено (с точностью до гомотопий) непрерывное отображение
) определено (с точностью до гомотопий) непрерывное отображение  . Таким образом, объекту Xсопоставляется проективная система топологич. пространств
. Таким образом, объекту Xсопоставляется проективная система топологич. пространств  , где
, где  - семейство всех покрытий объекта X.
- семейство всех покрытий объекта X. . Это - снова симплициальный объект K, в топологизированной категории
. Это - снова симплициальный объект K, в топологизированной категории  с финальным объектом X, удовлетворяющий условиям:
с финальным объектом X, удовлетворяющий условиям:  - покрытие объекта X;для любого пканонич. морфизм
- покрытие объекта X;для любого пканонич. морфизм 
 является покрытием, где
является покрытием, где 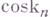 - функтор п- гокоскелета.
- функтор п- гокоскелета. приводит к проективной системе пространств, параметризованной гиперпокрытиями.
приводит к проективной системе пространств, параметризованной гиперпокрытиями. с финальным объектом X. Группы гомотопий, гомологии и когомологий вводятся стандартным способом.
с финальным объектом X. Группы гомотопий, гомологии и когомологий вводятся стандартным способом. на схеме X. В этом случае Г. т. схемы Xпредставляет собой прообъект категории пунктированных симплициальных множеств или категории конечных клеточных комплексов. Определяемые для таких объектов гомотопические группы
на схеме X. В этом случае Г. т. схемы Xпредставляет собой прообъект категории пунктированных симплициальных множеств или категории конечных клеточных комплексов. Определяемые для таких объектов гомотопические группы  являются проконечнымн группами и наз. i-ми гомотопическими группами схемы X(см. [2]). Если X - нормальная схема, то
являются проконечнымн группами и наз. i-ми гомотопическими группами схемы X(см. [2]). Если X - нормальная схема, то  совпадает с фундаментальной группой схемы, определяемой по Гротен-дику [3]. Г. т. точки
совпадает с фундаментальной группой схемы, определяемой по Гротен-дику [3]. Г. т. точки 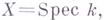 где
где 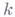 - поле, совпадает с проективным пределом пространств Эйленберга - Маклейна
- поле, совпадает с проективным пределом пространств Эйленберга - Маклейна  где
где  - группа Галуа конечного расширения Галуа
- группа Галуа конечного расширения Галуа  поля
поля 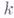 . В случае алгебраич. многообразий над полем комплексных чисел
. В случае алгебраич. многообразий над полем комплексных чисел  имеет место теорема сравнения: группы
имеет место теорема сравнения: группы  являются проконечным пополнением обычных гомотопич. групп
являются проконечным пополнением обычных гомотопич. групп  комплексного пространства Х ап, ассоциированного с X.
комплексного пространства Х ап, ассоциированного с X.