"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОТОПИЧЕСКИЙ ТИП
Значение ГОМОТОПИЧЕСКИЙ ТИП в математической энциклопедии:
класс гомотопически эквивалентных топологич. пространств. Отображения  и
и  наз. взаимно обратными гомотопическими эквивалентностями, если
наз. взаимно обратными гомотопическими эквивалентностями, если  и
и  Если выполнено только первое из этих соотношений, то gназ. гомотопически мономорфным отображением, а f - гомотопически эпиморфным отображением. Отображение тогда и только тогда является гомотопич. эквивалентностью, когда оно гомо-топпчески мономорфно и эпиморфно. Если существует гомотопически эпиморфное отображение
Если выполнено только первое из этих соотношений, то gназ. гомотопически мономорфным отображением, а f - гомотопически эпиморфным отображением. Отображение тогда и только тогда является гомотопич. эквивалентностью, когда оно гомо-топпчески мономорфно и эпиморфно. Если существует гомотопически эпиморфное отображение  то говорят, что пространство Yдоминирует над пространством X. Если существует гомотопич. эквивалентность
то говорят, что пространство Yдоминирует над пространством X. Если существует гомотопич. эквивалентность  , то пространства X и Y иаз. гомотопически эквивалентными, или пространствами одного гомотопического типа.
, то пространства X и Y иаз. гомотопически эквивалентными, или пространствами одного гомотопического типа.
Проблема гомотопического типа состоит в нахождении необходимых и достаточных условий гомотопич. эквивалентности любых пространств. Оказывается удобным эту постановку несколько ослабить. Отображение  наз. слабой гомотопической эквивалентностью, если оно индуцирует изоморфизм гомотопических групп всех размерностей. Соответственно, пространства Xи Y наз. слабо гомотопически эквивалентными, если существует либо слабая гомотопич. эквивалентность
наз. слабой гомотопической эквивалентностью, если оно индуцирует изоморфизм гомотопических групп всех размерностей. Соответственно, пространства Xи Y наз. слабо гомотопически эквивалентными, если существует либо слабая гомотопич. эквивалентность  либо слабая гомотопич. эквивалентность
либо слабая гомотопич. эквивалентность  . Поскольку любая гомотопич. эквивалентность является слабой гомотопич. эквивалентностью, то гомотопически эквивалентные пространства слабо гомотопически эквивалентны.
. Поскольку любая гомотопич. эквивалентность является слабой гомотопич. эквивалентностью, то гомотопически эквивалентные пространства слабо гомотопически эквивалентны.
Обратное верно, если пространства являются клеточными разбиениями (теорема Уайтхеда). Эта теорема основана на том, что: 1) отображение  тогда и только тогда является гомотопич. эквивалентностью, когда Xесть деформационный ретракт цилиндра
тогда и только тогда является гомотопич. эквивалентностью, когда Xесть деформационный ретракт цилиндра  отображения f; 2) отображение
отображения f; 2) отображение  тогда и только тогда является слабой гомотопич. эквивалентностью, когда подпространство Xцилиндра М f гомотопически репрезентативно (см. Репрезентативное подпространство);3) подразбиение клеточного разбиения тогда и только тогда репрезентативно, когда оно является деформационным ретрактом.
тогда и только тогда является слабой гомотопич. эквивалентностью, когда подпространство Xцилиндра М f гомотопически репрезентативно (см. Репрезентативное подпространство);3) подразбиение клеточного разбиения тогда и только тогда репрезентативно, когда оно является деформационным ретрактом.
Таким образом, проблема Г. т. на категории клеточных разбиений равносильна проблеме слабого Г. т. С другой стороны, любое пространство Xслабо гомотопически эквивалентно геометрич. реализации его сингулярного симплициального множества  . Поэтому в проблеме слабого Г. т. без ограничения общности можно рассматривать лишь клеточные разбиения.
. Поэтому в проблеме слабого Г. т. без ограничения общности можно рассматривать лишь клеточные разбиения.
Отображения  наз. n-гомотопными, если для любого клеточного разбиения Кразмерности
наз. n-гомотопными, если для любого клеточного разбиения Кразмерности  и любого отображения
и любого отображения 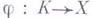 отображения
отображения  и
и  гомотопны. Если X - клеточное разбиение, это имеет место тогда и только тогда, когда
гомотопны. Если X - клеточное разбиение, это имеет место тогда и только тогда, когда  Пространства, эквивалентные по отношению n-гомотопности, наз. пространствами одного n-гомотопического типа. Клеточные разбиения Ки Lназ. разбиениями одного п- типа (обозначение
Пространства, эквивалентные по отношению n-гомотопности, наз. пространствами одного n-гомотопического типа. Клеточные разбиения Ки Lназ. разбиениями одного п- типа (обозначение  ), если их n-е остовы
), если их n-е остовы  и
и  имеют один и тот же
имеют один и тот же  - гомотопический тип. Если
- гомотопический тип. Если  при любом
при любом  .
.
Это остается справедливым и при  , если под
, если под  -типом понимать Г. т. Другими словами, понятие n-типа гомотопически инвариантно. Важность понятия n-типа для проблемы Г. т. определяется тем, что два n-мерных клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда они имеют один и тот же (n+1)-тип.
-типом понимать Г. т. Другими словами, понятие n-типа гомотопически инвариантно. Важность понятия n-типа для проблемы Г. т. определяется тем, что два n-мерных клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда они имеют один и тот же (n+1)-тип.
Пусть X - произвольное пространство (для простоты - линейно связное). Симплициальное подмножество М(X).симплициального множества S(X).наз. минимальны м, если оно содержит все сингулярные симплексы, являющиеся отображениями в нек-рую фиксированную точку  , и если для любого симплекса
, и если для любого симплекса  , все грани к-рого принадлежат подмножеству М(Х), в М(X).существует единственный симплекс, гомотопный s(относительно границы стандартного симплекса). Минимальные подмножества существуют и, с точностью до изоморфизма, однозначно определяются пространством X. При этом два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их минимальные симплициальные множества изоморфны. Таким образом, для решения проблемы слабого Г. т. остается лишь найти достаточно удовлетворительное описание симплициальных множеств М(Х).
, все грани к-рого принадлежат подмножеству М(Х), в М(X).существует единственный симплекс, гомотопный s(относительно границы стандартного симплекса). Минимальные подмножества существуют и, с точностью до изоморфизма, однозначно определяются пространством X. При этом два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их минимальные симплициальные множества изоморфны. Таким образом, для решения проблемы слабого Г. т. остается лишь найти достаточно удовлетворительное описание симплициальных множеств М(Х).
Пусть  есть
есть  -мерный стандартный симплекс, рассматриваемый как симплициальное разбиение (относительно его, стандартной триангуляции) и пусть
-мерный стандартный симплекс, рассматриваемый как симплициальное разбиение (относительно его, стандартной триангуляции) и пусть  - группа его n-мерных коцепей над абслевой группой
- группа его n-мерных коцепей над абслевой группой  (точнее, группа нормализованных n-мерных коцепей симплициального множества
(точнее, группа нормализованных n-мерных коцепей симплициального множества  ). Пусть
). Пусть  - симплициальное множество, в к-ром симплексами размерности qявляются коцепи из
- симплициальное множество, в к-ром симплексами размерности qявляются коцепи из  , а операторы грани
, а операторы грани  и вырождения
и вырождения 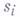 являются коцепными отображениями, индуцированными стандартными симплициальными отображениями
являются коцепными отображениями, индуцированными стандартными симплициальными отображениями  и
и  (отображение
(отображение  "выпускает" i-ю вершину, а отображение
"выпускает" i-ю вершину, а отображение  "склеивает" г-ю и
"склеивает" г-ю и  -ю вершины). Симплексы, являющиеся коциклами, образуют в
-ю вершины). Симплексы, являющиеся коциклами, образуют в 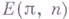 некоторое симплициальное подмножество
некоторое симплициальное подмножество  . Кограничный оператор
. Кограничный оператор 
 . определяет симплициальное отображение
. определяет симплициальное отображение  ядром к-рого служит подмножество
ядром к-рого служит подмножество  . Отображение
. Отображение  является расслоением (в смысле Кана) со слоем
является расслоением (в смысле Кана) со слоем  . Кроме того, симплициальное множество
. Кроме того, симплициальное множество  является в категории симплициальных множеств объектом типа
является в категории симплициальных множеств объектом типа  (по отношению к гомотопич. группам в смысле Кана, см. дйленберга - Маклейна пространство), а симплициальное множество
(по отношению к гомотопич. группам в смысле Кана, см. дйленберга - Маклейна пространство), а симплициальное множество  гомотопически тривиально (гомотопически эквивалентно "точке"). Таким образом, расслоение
гомотопически тривиально (гомотопически эквивалентно "точке"). Таким образом, расслоение  является симплициальным аналогом Серра расслоения путей над пространством типа
является симплициальным аналогом Серра расслоения путей над пространством типа  .
.
Симплициальное множество  при
при  имеет смысл и для любой (не обязательно абелевой) группы
имеет смысл и для любой (не обязательно абелевой) группы  . Получающееся симплициальное множество
. Получающееся симплициальное множество  есть не что иное, как стандартная симплициальная резольвента группы
есть не что иное, как стандартная симплициальная резольвента группы  .
.
Пусть  - мультипликативная группа операторов аддитивной группы
- мультипликативная группа операторов аддитивной группы  . Для любого коцикла апроизвольного симплициального множества
. Для любого коцикла апроизвольного симплициального множества  над группой
над группой  в группе коцепей этого множества над группой
в группе коцепей этого множества над группой  определен кограничный оператор
определен кограничный оператор  относительно коцикла а. Пусть
относительно коцикла а. Пусть  - произвольный g-мерный симплекс из Nи пусть
- произвольный g-мерный симплекс из Nи пусть  - его характеристическое отображение (см. Симплициалъное множество). Тогда в
- его характеристическое отображение (см. Симплициалъное множество). Тогда в  определен коцикл
определен коцикл  . Пусть кограничный оператор относительно этого коцикла обозначен символом
. Пусть кограничный оператор относительно этого коцикла обозначен символом  . Пусть
. Пусть  - произвольный (n+1)-мерный коцикл симплициального множества Nнад группой p относительно коцикла а. Если в прямом произведении симплициальных множеств
- произвольный (n+1)-мерный коцикл симплициального множества Nнад группой p относительно коцикла а. Если в прямом произведении симплициальных множеств  рассмотреть подмножество
рассмотреть подмножество 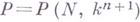 , состоящее из всевозможных пар
, состоящее из всевозможных пар  для к-рых
для к-рых 
 то Рбудет симплициальным подмножеством. Формула
то Рбудет симплициальным подмножеством. Формула  определяет надъективное (сюръективное) отображение
определяет надъективное (сюръективное) отображение  являющееся расслоением (в смысле Кана). Это расслоение будет обозначаться
являющееся расслоением (в смысле Кана). Это расслоение будет обозначаться  В случае, когда коцикл а тривиален, это есть не что иное как расслоение, индуцированное симплициальным отображением
В случае, когда коцикл а тривиален, это есть не что иное как расслоение, индуцированное симплициальным отображением  отвечающим коциклу
отвечающим коциклу  , из расслоения
, из расслоения 
Над n-мерным остовом  симплициального множества
симплициального множества  расслоение робладает сечением
расслоение робладает сечением , и коцикл
, и коцикл 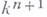 является препятствием к распространению этого сечения на
является препятствием к распространению этого сечения на  . После отождествления симплексов
. После отождествления симплексов  и
и  можно считать, что
можно считать, что  . При этом
. При этом  .
.
Пусть теперь имеется последовательность расслоений симплициальных множеств

начальный член 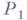 к-рой является симплициальным множеством
к-рой является симплициальным множеством  , построенным для мультипликативной группы
, построенным для мультипликативной группы  . По определению, одномерные симплексы из
. По определению, одномерные симплексы из  находятся в естественном биективном соответствии с элементами группы
находятся в естественном биективном соответствии с элементами группы  . Сопоставление каждому такому симплексу соответствующего элемента группы
. Сопоставление каждому такому симплексу соответствующего элемента группы  приводит в
приводит в  к нек-рому одномерному коциклу
к нек-рому одномерному коциклу  над группой
над группой  . Пусть коцикл
. Пусть коцикл  определяется в Р п индуктивной формулой
определяется в Р п индуктивной формулой  Последовательность (1) наз. гомотопической резольвентой, или Постникова системой (первоначальное название - натуральная система), если для любого
Последовательность (1) наз. гомотопической резольвентой, или Постникова системой (первоначальное название - натуральная система), если для любого  симплициальное множество
симплициальное множество  есть множество вида
есть множество вида  - коцикл размерности
- коцикл размерности  в
в  над нек-рой
над нек-рой  -группой
-группой  относительно коцикла а п[и расслоение р n есть расслоение
относительно коцикла а п[и расслоение р n есть расслоение  ]. Эта последовательность наз. резольвентой симплициального множeства М, если для любого
]. Эта последовательность наз. резольвентой симплициального множeства М, если для любого  задано симплициальное отображение
задано симплициальное отображение  являющееся изоморфизмом
являющееся изоморфизмом
на  и такое, что
и такое, что  Резольвента определяет спмплпциальное множество Моднозначно с точностью до изоморфизма. С другой стороны, сама резольвента однозначно определяется группами
Резольвента определяет спмплпциальное множество Моднозначно с точностью до изоморфизма. С другой стороны, сама резольвента однозначно определяется группами 
 и коциклами
и коциклами  Поэтому резольвентой можно называть также и объект
Поэтому резольвентой можно называть также и объект  состоящий из групп
состоящий из групп  и коциклов
и коциклов  Не всякое симплициальное множество Мобладает резольвентой. Основная теорема теории гомотопич. резольвент утверждает, что симплициальное множество Мтогда и только тогда обладает резольвентой, когда оно изоморфно минимальному симплициальному множеству М (X).нек-рого топологич. пространства X. При этом
Не всякое симплициальное множество Мобладает резольвентой. Основная теорема теории гомотопич. резольвент утверждает, что симплициальное множество Мтогда и только тогда обладает резольвентой, когда оно изоморфно минимальному симплициальному множеству М (X).нек-рого топологич. пространства X. При этом  .
.
Резольвента минимального множества  строится следующим образом. Пусть а - произвольный q-мерный симплекс из
строится следующим образом. Пусть а - произвольный q-мерный симплекс из  . Этот симплекс представляет собой отображение
. Этот симплекс представляет собой отображение  , переводящее все вершины симплекса
, переводящее все вершины симплекса  в точку
в точку  . Поэтому на любой одномерной грани (ребре) симплекса
. Поэтому на любой одномерной грани (ребре) симплекса  оно определяет нек-рый элемент группы
оно определяет нек-рый элемент группы  . Таким образом на
. Таким образом на  возникает нек-рый одномерный коцикл над группой
возникает нек-рый одномерный коцикл над группой  , т. е. q-мерный симплекс из
, т. е. q-мерный симплекс из  ; он будет обозначаться
; он будет обозначаться  . Тем самым получено нек-рое (симплициальное) отображение
. Тем самым получено нек-рое (симплициальное) отображение  . Это отображение является изоморфизмом на
. Это отображение является изоморфизмом на  и эпиморфизмом на
и эпиморфизмом на  . Далее проводится индукция: пусть для нек-рого
. Далее проводится индукция: пусть для нек-рого  уже построено симплицнальное множество
уже построено симплицнальное множество  и симплпцнальное отображение
и симплпцнальное отображение  являющееся изоморфизмом на
являющееся изоморфизмом на  и эпиморфизмом на
и эпиморфизмом на  . Для отображения
. Для отображения  существует обратное справа отображение
существует обратное справа отображение  Пусть
Пусть  - препятствие к распространению этого отображения на
- препятствие к распространению этого отображения на  Препятствие
Препятствие  является
является  -мерным коциклом в
-мерным коциклом в  над группой
над группой  относительно коцикла
относительно коцикла  Для любого
Для любого  -мерного симплекса t из Мсимплекс
-мерного симплекса t из Мсимплекс  сравним с t, и потому определен различающий элемент
сравним с t, и потому определен различающий элемент  (см. Различающая). Пусть
(см. Различающая). Пусть  - произвольный q-мерный симплекс из М. На каждой
- произвольный q-мерный симплекс из М. На каждой  -мерной грани симплекса
-мерной грани симплекса  он определяет некоторый
он определяет некоторый  -мерный симплекс
-мерный симплекс  . Сопоставление этой грани элемента
. Сопоставление этой грани элемента  приводит к некоторой
приводит к некоторой  -мерной коцепи в
-мерной коцепи в  над
над  , то есть к некоторому g-мерному симплексу
, то есть к некоторому g-мерному симплексу  симплициаль-ного множества
симплициаль-ного множества  Пара
Пара 
 принадлежит симплициальному множеству
принадлежит симплициальному множеству 
 Для завершения индукции остается заметить, что построенное отображение
Для завершения индукции остается заметить, что построенное отображение  симплициально, является изоморфизмом на
симплициально, является изоморфизмом на  и эпиморфизмом на
и эпиморфизмом на 
Резольвента  строится по симплициальному множеству
строится по симплициальному множеству  неоднозначно: имеется произвол в выборе обратных отображений
неоднозначно: имеется произвол в выборе обратных отображений  . Проще всего описать эту неоднозначность, понимая резольвенты в смысле (1). Именно, две такие резольвенты
. Проще всего описать эту неоднозначность, понимая резольвенты в смысле (1). Именно, две такие резольвенты  и
и  тогда и только тогда возникают из одного минимального симплициального множества
тогда и только тогда возникают из одного минимального симплициального множества  , когда они изоморфны как последовательности отображений, т. е. когда для любого
, когда они изоморфны как последовательности отображений, т. е. когда для любого  существует такой изоморфизм
существует такой изоморфизм 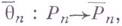 что
что  Чтобы описать этот изоморфизм в терминах резольвент
Чтобы описать этот изоморфизм в терминах резольвент  и
и  , следует заметить, что существование изоморфизма
, следует заметить, что существование изоморфизма  равносильно существованию изоморфизма групп
равносильно существованию изоморфизма групп  При этом
При этом  Далее, для изоморфизма
Далее, для изоморфизма  тогда и только тогда существует следующий изоморфизм
тогда и только тогда существует следующий изоморфизм  когда существует такой
когда существует такой  -изоморфизм
-изоморфизм  (см. Операторный гомоморфизм). и такая коцепь
(см. Операторный гомоморфизм). и такая коцепь 
 что
что

При этом изоморфизм  определяется формулой
определяется формулой

Резольвенты  и
и  тогда и только тогда возникают из одного минимального симплициального множества, когда существуют такие изоморфизмы
тогда и только тогда возникают из одного минимального симплициального множества, когда существуют такие изоморфизмы  являющиеся при
являющиеся при  -изоморфизмами, что для любого
-изоморфизмами, что для любого  выполнены соотношения (2), где
выполнены соотношения (2), где  - изоморфизм, последовательно определяемый при
- изоморфизм, последовательно определяемый при  формулой (2'), а при п=1являющийся изоморфизмом, индуцированным изоморфизмом
формулой (2'), а при п=1являющийся изоморфизмом, индуцированным изоморфизмом  . В этом случае резольвенты
. В этом случае резольвенты  и
и  наз. изоморфными. Гомотопической резольвентой пространства Xназ. резольвента симплпциального множества М(Х). Резюмируя, получаем, что два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их гомотопич. резольвенты изоморфны; в частности, два клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда их гомотопические резольвенты изоморфны.
наз. изоморфными. Гомотопической резольвентой пространства Xназ. резольвента симплпциального множества М(Х). Резюмируя, получаем, что два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их гомотопич. резольвенты изоморфны; в частности, два клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда их гомотопические резольвенты изоморфны.
Если условия (2) выполнены только при  , то изоморфизмы
, то изоморфизмы  существуют только при
существуют только при  . В этом случае говорят, что данные резольвенты m-изоморфны. Два клеточных разбиения тогда и только тогда имеют один и тот же re-тип, когда их гомотопич. резольвенты ( п-1)-изоморфны.
. В этом случае говорят, что данные резольвенты m-изоморфны. Два клеточных разбиения тогда и только тогда имеют один и тот же re-тип, когда их гомотопич. резольвенты ( п-1)-изоморфны.
Изложенное решение проблемы Г. т. (и n-типа) позволяет доказывать целый ряд общих теорем и существенно проясняет принципиальную сторону дела (но явное вычисление резольвент возможно лишь в немногих случаях). Из него вытекает, что для любого односвязного пространства с конечными группами гомологии гомотопич. группы могут быть эффективно вычислены. Аналогичное утверждение справедливо и для пространств, группы гомологии к-рых лишь конечно порождены (см. [2]). Тот факт, что Г. т. полностью определяется резольвентой, показывает, что любая задача теории гомотопий сводится к нек-рому утверждению о резольвентах соответствующих пространств. Это позволяет классифицировать задачи по числу коциклов  , участвующих в их решении. Если рассматриваемое пространство
, участвующих в их решении. Если рассматриваемое пространство  связно, то его резольвента начинается фактически с члена
связно, то его резольвента начинается фактически с члена  . Если решение данной задачи может быть сформулировано лишь с использованием первой нетривиальной группы pn , то эта задача наз. задачей нулевой ступени [напр., задача Хойфа - Уитни о классификации отображений n-мерного полиэдра в
. Если решение данной задачи может быть сформулировано лишь с использованием первой нетривиальной группы pn , то эта задача наз. задачей нулевой ступени [напр., задача Хойфа - Уитни о классификации отображений n-мерного полиэдра в  -связное пространство]. Если для этого требуются группы
-связное пространство]. Если для этого требуются группы  и коцикл
и коцикл  , то задача наз. задачей первой ступени [напр., задача о классификации отображений
, то задача наз. задачей первой ступени [напр., задача о классификации отображений  -мерного полиэдра в
-мерного полиэдра в  -связное пространство]. Аналогично определяются задачи второй, третьей и т. д. ступеней. Известны эффективные решения любых задач нулевой и первой ступеней. Это связано с тем, что для любого
-связное пространство]. Аналогично определяются задачи второй, третьей и т. д. ступеней. Известны эффективные решения любых задач нулевой и первой ступеней. Это связано с тем, что для любого  -связного пространства можно вполне эффективно вычислить класс когомологий коцикла
-связного пространства можно вполне эффективно вычислить класс когомологий коцикла  ; именно, он имеет вид
; именно, он имеет вид  , где
, где  - фундаментальный класс пространства
- фундаментальный класс пространства  а
а  - при
- при  - Стинрода операция, соответствующая естественному спариванию
- Стинрода операция, соответствующая естественному спариванию  а при
а при  - некоторый ее вариант, известный как Понтрягина квадрат. Для задач высших ступеней необходимо аналогичное эффективное вычисление следующих коциклов
- некоторый ее вариант, известный как Понтрягина квадрат. Для задач высших ступеней необходимо аналогичное эффективное вычисление следующих коциклов  ,
, 
фундаментального класса с применением нек-рой когомологической операции соответствующего порядка. Это, в частности, показывает, что решение любой задачи теории гомотопий может быть сформулировано в терминах определенных когомологич. операций. Однако ввиду большой сложности операций высших порядков получены лишь решения отдельных задач высших ступеней, использующие соображения специального характера. Нек-рый общий прогресс достигнут в предположении стационарности: продвинутое в этих предположениях уже довольно далеко вычисление дифференциалов спектральной последовательности Адамса равносильно вычислению нек-рых стационарных операций высоких порядков.
Теория гомотопич. резольвент может быть переформулирована в следующей, "геометризованной" форме. Резольвентой наз. произвольная последовательность расслоений в смысле Серра

в к-рой каждое пространство  обладает тем свойством, что
обладает тем свойством, что  при
при  . Эта последовательность наз. резольвентой пространства X, если для любого
. Эта последовательность наз. резольвентой пространства X, если для любого  заданы отображения
заданы отображения  индуцирующие изоморфизм гомотопич. групп до размерности пи такие, что
индуцирующие изоморфизм гомотопич. групп до размерности пи такие, что  Эта резольвента с точностью до изоморфизма [понимаемого как изоморфизм последовательностей (см. Последовательностей категория)]определяется однозначно группами
Эта резольвента с точностью до изоморфизма [понимаемого как изоморфизм последовательностей (см. Последовательностей категория)]определяется однозначно группами  и характеристич. классами
и характеристич. классами  расслоений
расслоений  . Резольвента существует для любого линейно связного пространства X[таковой будет, напр., геометрическая реализация "алгебраической" резольвенты (1)] и определяет это пространство с точностью до слабой гомотопич. эквивалентности. Слоем расслоения
. Резольвента существует для любого линейно связного пространства X[таковой будет, напр., геометрическая реализация "алгебраической" резольвенты (1)] и определяет это пространство с точностью до слабой гомотопич. эквивалентности. Слоем расслоения  является пространство типа
является пространство типа  , и в случае, когда Xгомотопически re-просто (см. Гомотопическая группа), напр., односвязно, это расслоение индуцировано из Серра расслоения путей над пространством
, и в случае, когда Xгомотопически re-просто (см. Гомотопическая группа), напр., односвязно, это расслоение индуцировано из Серра расслоения путей над пространством  посредством нек-рого отображения
посредством нек-рого отображения 
 представляющего (см. Эйленберга - Маклейна пространство, Представимый функтор). класс когомологий
представляющего (см. Эйленберга - Маклейна пространство, Представимый функтор). класс когомологий  .
.
Если пространство  -связно, то его резольвента фактически начинается с члена
-связно, то его резольвента фактически начинается с члена  При
При  удобно наряду с "абсолютными" резольвентами (3) рассматривать также так наз. резольвенты по модулю простого числа р, определение к-рых отличается от определения резольвент (3) только тем, что гомотопич. группы заменяются их р-компонентами. Если для Xнайдены резольвенты по любому простому модулю р, нахождение "абсолютной" резольвенты, как правило, не представляет труда. Поэтому в задаче вычисления резольвент (включающей задачу вычисления гомотопич. групп) обычно ограничиваются "модульными" резольвентами, в вычислении к-рых могут быть использованы мощные методы теории спектральных последовательностей и теории когомологич. операций. Для нек-рых пространств-вычисление резольвент далеко продвинуто.
удобно наряду с "абсолютными" резольвентами (3) рассматривать также так наз. резольвенты по модулю простого числа р, определение к-рых отличается от определения резольвент (3) только тем, что гомотопич. группы заменяются их р-компонентами. Если для Xнайдены резольвенты по любому простому модулю р, нахождение "абсолютной" резольвенты, как правило, не представляет труда. Поэтому в задаче вычисления резольвент (включающей задачу вычисления гомотопич. групп) обычно ограничиваются "модульными" резольвентами, в вычислении к-рых могут быть использованы мощные методы теории спектральных последовательностей и теории когомологич. операций. Для нек-рых пространств-вычисление резольвент далеко продвинуто.
Например, для сферы  (при пдостаточно большом, чтобы выполнялись условия стационарности) известно уже довольно много первых членов ее резольвенты по модулю 2. Достаточно описать соответствующие группы
(при пдостаточно большом, чтобы выполнялись условия стационарности) известно уже довольно много первых членов ее резольвенты по модулю 2. Достаточно описать соответствующие группы  [то есть 2-компоненты групп
[то есть 2-компоненты групп  ] и классы когомологий
] и классы когомологий  . Первые группы
. Первые группы 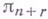 имеют следующий вид
имеют следующий вид

Класс  имеет вид
имеет вид  где
где 
 - фундаментальный класс. Следующий класс
- фундаментальный класс. Следующий класс  обладает тем свойством, что на слое
обладает тем свойством, что на слое  расслоения
расслоения  он высекает класс
он высекает класс  и однозначно этим свойством характеризуется. Аналогично, класс
и однозначно этим свойством характеризуется. Аналогично, класс 
 однозначно характеризуется тем, что после приведения по модулю 2 он переходит в класс
однозначно характеризуется тем, что после приведения по модулю 2 он переходит в класс  Классы
Классы  и
и  равны нулю, а класс
равны нулю, а класс  однозначно характеризуется тем, что на слое
однозначно характеризуется тем, что на слое  расслоения
расслоения  он высекает класс
он высекает класс  . Наконец, класс
. Наконец, класс  характеризуется тем, что после приведения по модулю 2 он переходит в класс
характеризуется тем, что после приведения по модулю 2 он переходит в класс  .
.
Лит.:[1]Постников М. <М., Исследования по гомотопической теории непрерывных отображений, ч. 1, Алгебраическая теория систем, ч. 2, Натуральная система и гомотопический тип, М., 1955; [2] Браун Э. X., "Математика", 1958, 2:2, с. 3-24; [3] Мошер Р., Тангора М., Когомологические операции и их приложения в теории гомотопий, пер. с англ., М., 1970, гл. 13, М. М. Постников.

 и
и  наз. взаимно обратными гомотопическими эквивалентностями, если
наз. взаимно обратными гомотопическими эквивалентностями, если  и
и  Если выполнено только первое из этих соотношений, то gназ. гомотопически мономорфным отображением, а f - гомотопически эпиморфным отображением. Отображение тогда и только тогда является гомотопич. эквивалентностью, когда оно гомо-топпчески мономорфно и эпиморфно. Если существует гомотопически эпиморфное отображение
Если выполнено только первое из этих соотношений, то gназ. гомотопически мономорфным отображением, а f - гомотопически эпиморфным отображением. Отображение тогда и только тогда является гомотопич. эквивалентностью, когда оно гомо-топпчески мономорфно и эпиморфно. Если существует гомотопически эпиморфное отображение  то говорят, что пространство Yдоминирует над пространством X. Если существует гомотопич. эквивалентность
то говорят, что пространство Yдоминирует над пространством X. Если существует гомотопич. эквивалентность  , то пространства X и Y иаз. гомотопически эквивалентными, или пространствами одного гомотопического типа.
, то пространства X и Y иаз. гомотопически эквивалентными, или пространствами одного гомотопического типа. наз. слабой гомотопической эквивалентностью, если оно индуцирует изоморфизм гомотопических групп всех размерностей. Соответственно, пространства Xи Y наз. слабо гомотопически эквивалентными, если существует либо слабая гомотопич. эквивалентность
наз. слабой гомотопической эквивалентностью, если оно индуцирует изоморфизм гомотопических групп всех размерностей. Соответственно, пространства Xи Y наз. слабо гомотопически эквивалентными, если существует либо слабая гомотопич. эквивалентность  либо слабая гомотопич. эквивалентность
либо слабая гомотопич. эквивалентность  . Поскольку любая гомотопич. эквивалентность является слабой гомотопич. эквивалентностью, то гомотопически эквивалентные пространства слабо гомотопически эквивалентны.
. Поскольку любая гомотопич. эквивалентность является слабой гомотопич. эквивалентностью, то гомотопически эквивалентные пространства слабо гомотопически эквивалентны. тогда и только тогда является гомотопич. эквивалентностью, когда Xесть деформационный ретракт цилиндра
тогда и только тогда является гомотопич. эквивалентностью, когда Xесть деформационный ретракт цилиндра  отображения f; 2) отображение
отображения f; 2) отображение  тогда и только тогда является слабой гомотопич. эквивалентностью, когда подпространство Xцилиндра М f гомотопически репрезентативно (см. Репрезентативное подпространство);3) подразбиение клеточного разбиения тогда и только тогда репрезентативно, когда оно является деформационным ретрактом.
тогда и только тогда является слабой гомотопич. эквивалентностью, когда подпространство Xцилиндра М f гомотопически репрезентативно (см. Репрезентативное подпространство);3) подразбиение клеточного разбиения тогда и только тогда репрезентативно, когда оно является деформационным ретрактом. . Поэтому в проблеме слабого Г. т. без ограничения общности можно рассматривать лишь клеточные разбиения.
. Поэтому в проблеме слабого Г. т. без ограничения общности можно рассматривать лишь клеточные разбиения. наз. n-гомотопными, если для любого клеточного разбиения Кразмерности
наз. n-гомотопными, если для любого клеточного разбиения Кразмерности  и любого отображения
и любого отображения 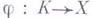 отображения
отображения  и
и  гомотопны. Если X - клеточное разбиение, это имеет место тогда и только тогда, когда
гомотопны. Если X - клеточное разбиение, это имеет место тогда и только тогда, когда  Пространства, эквивалентные по отношению n-гомотопности, наз. пространствами одного n-гомотопического типа. Клеточные разбиения Ки Lназ. разбиениями одного п- типа (обозначение
Пространства, эквивалентные по отношению n-гомотопности, наз. пространствами одного n-гомотопического типа. Клеточные разбиения Ки Lназ. разбиениями одного п- типа (обозначение  ), если их n-е остовы
), если их n-е остовы  и
и  имеют один и тот же
имеют один и тот же  - гомотопический тип. Если
- гомотопический тип. Если  при любом
при любом  .
. , если под
, если под  -типом понимать Г. т. Другими словами, понятие n-типа гомотопически инвариантно. Важность понятия n-типа для проблемы Г. т. определяется тем, что два n-мерных клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда они имеют один и тот же (n+1)-тип.
-типом понимать Г. т. Другими словами, понятие n-типа гомотопически инвариантно. Важность понятия n-типа для проблемы Г. т. определяется тем, что два n-мерных клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда они имеют один и тот же (n+1)-тип. , и если для любого симплекса
, и если для любого симплекса  , все грани к-рого принадлежат подмножеству М(Х), в М(X).существует единственный симплекс, гомотопный s(относительно границы стандартного симплекса). Минимальные подмножества существуют и, с точностью до изоморфизма, однозначно определяются пространством X. При этом два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их минимальные симплициальные множества изоморфны. Таким образом, для решения проблемы слабого Г. т. остается лишь найти достаточно удовлетворительное описание симплициальных множеств М(Х).
, все грани к-рого принадлежат подмножеству М(Х), в М(X).существует единственный симплекс, гомотопный s(относительно границы стандартного симплекса). Минимальные подмножества существуют и, с точностью до изоморфизма, однозначно определяются пространством X. При этом два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их минимальные симплициальные множества изоморфны. Таким образом, для решения проблемы слабого Г. т. остается лишь найти достаточно удовлетворительное описание симплициальных множеств М(Х). есть
есть  -мерный стандартный симплекс, рассматриваемый как симплициальное разбиение (относительно его, стандартной триангуляции) и пусть
-мерный стандартный симплекс, рассматриваемый как симплициальное разбиение (относительно его, стандартной триангуляции) и пусть  - группа его n-мерных коцепей над абслевой группой
- группа его n-мерных коцепей над абслевой группой  (точнее, группа нормализованных n-мерных коцепей симплициального множества
(точнее, группа нормализованных n-мерных коцепей симплициального множества  ). Пусть
). Пусть  - симплициальное множество, в к-ром симплексами размерности qявляются коцепи из
- симплициальное множество, в к-ром симплексами размерности qявляются коцепи из  , а операторы грани
, а операторы грани  и вырождения
и вырождения 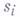 являются коцепными отображениями, индуцированными стандартными симплициальными отображениями
являются коцепными отображениями, индуцированными стандартными симплициальными отображениями  и
и  (отображение
(отображение  "выпускает" i-ю вершину, а отображение
"выпускает" i-ю вершину, а отображение  "склеивает" г-ю и
"склеивает" г-ю и  -ю вершины). Симплексы, являющиеся коциклами, образуют в
-ю вершины). Симплексы, являющиеся коциклами, образуют в 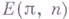 некоторое симплициальное подмножество
некоторое симплициальное подмножество  . Кограничный оператор
. Кограничный оператор 
 . определяет симплициальное отображение
. определяет симплициальное отображение  ядром к-рого служит подмножество
ядром к-рого служит подмножество  . Отображение
. Отображение  является расслоением (в смысле Кана) со слоем
является расслоением (в смысле Кана) со слоем  . Кроме того, симплициальное множество
. Кроме того, симплициальное множество  является в категории симплициальных множеств объектом типа
является в категории симплициальных множеств объектом типа  (по отношению к гомотопич. группам в смысле Кана, см. дйленберга - Маклейна пространство), а симплициальное множество
(по отношению к гомотопич. группам в смысле Кана, см. дйленберга - Маклейна пространство), а симплициальное множество  гомотопически тривиально (гомотопически эквивалентно "точке"). Таким образом, расслоение
гомотопически тривиально (гомотопически эквивалентно "точке"). Таким образом, расслоение  является симплициальным аналогом Серра расслоения путей над пространством типа
является симплициальным аналогом Серра расслоения путей над пространством типа  .
. при
при  имеет смысл и для любой (не обязательно абелевой) группы
имеет смысл и для любой (не обязательно абелевой) группы  . Получающееся симплициальное множество
. Получающееся симплициальное множество  есть не что иное, как стандартная симплициальная резольвента группы
есть не что иное, как стандартная симплициальная резольвента группы  .
. - мультипликативная группа операторов аддитивной группы
- мультипликативная группа операторов аддитивной группы  . Для любого коцикла апроизвольного симплициального множества
. Для любого коцикла апроизвольного симплициального множества  над группой
над группой  в группе коцепей этого множества над группой
в группе коцепей этого множества над группой  определен кограничный оператор
определен кограничный оператор  относительно коцикла а. Пусть
относительно коцикла а. Пусть  - произвольный g-мерный симплекс из Nи пусть
- произвольный g-мерный симплекс из Nи пусть  - его характеристическое отображение (см. Симплициалъное множество). Тогда в
- его характеристическое отображение (см. Симплициалъное множество). Тогда в  определен коцикл
определен коцикл  . Пусть кограничный оператор относительно этого коцикла обозначен символом
. Пусть кограничный оператор относительно этого коцикла обозначен символом  . Пусть
. Пусть  - произвольный (n+1)-мерный коцикл симплициального множества Nнад группой p относительно коцикла а. Если в прямом произведении симплициальных множеств
- произвольный (n+1)-мерный коцикл симплициального множества Nнад группой p относительно коцикла а. Если в прямом произведении симплициальных множеств  рассмотреть подмножество
рассмотреть подмножество 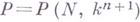 , состоящее из всевозможных пар
, состоящее из всевозможных пар  для к-рых
для к-рых 
 то Рбудет симплициальным подмножеством. Формула
то Рбудет симплициальным подмножеством. Формула  определяет надъективное (сюръективное) отображение
определяет надъективное (сюръективное) отображение  являющееся расслоением (в смысле Кана). Это расслоение будет обозначаться
являющееся расслоением (в смысле Кана). Это расслоение будет обозначаться  В случае, когда коцикл а тривиален, это есть не что иное как расслоение, индуцированное симплициальным отображением
В случае, когда коцикл а тривиален, это есть не что иное как расслоение, индуцированное симплициальным отображением  отвечающим коциклу
отвечающим коциклу  , из расслоения
, из расслоения 
 симплициального множества
симплициального множества  расслоение робладает сечением
расслоение робладает сечением , и коцикл
, и коцикл 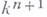 является препятствием к распространению этого сечения на
является препятствием к распространению этого сечения на  . После отождествления симплексов
. После отождествления симплексов  и
и  можно считать, что
можно считать, что  . При этом
. При этом  .
.
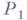 к-рой является симплициальным множеством
к-рой является симплициальным множеством  , построенным для мультипликативной группы
, построенным для мультипликативной группы  . По определению, одномерные симплексы из
. По определению, одномерные симплексы из  находятся в естественном биективном соответствии с элементами группы
находятся в естественном биективном соответствии с элементами группы  . Сопоставление каждому такому симплексу соответствующего элемента группы
. Сопоставление каждому такому симплексу соответствующего элемента группы  приводит в
приводит в  к нек-рому одномерному коциклу
к нек-рому одномерному коциклу  над группой
над группой  . Пусть коцикл
. Пусть коцикл  определяется в Р п индуктивной формулой
определяется в Р п индуктивной формулой  Последовательность (1) наз. гомотопической резольвентой, или Постникова системой (первоначальное название - натуральная система), если для любого
Последовательность (1) наз. гомотопической резольвентой, или Постникова системой (первоначальное название - натуральная система), если для любого  симплициальное множество
симплициальное множество  есть множество вида
есть множество вида  - коцикл размерности
- коцикл размерности  в
в  над нек-рой
над нек-рой  -группой
-группой  относительно коцикла а п[и расслоение р n есть расслоение
относительно коцикла а п[и расслоение р n есть расслоение  ]. Эта последовательность наз. резольвентой симплициального множeства М, если для любого
]. Эта последовательность наз. резольвентой симплициального множeства М, если для любого  задано симплициальное отображение
задано симплициальное отображение  являющееся изоморфизмом
являющееся изоморфизмом  и такое, что
и такое, что  Резольвента определяет спмплпциальное множество Моднозначно с точностью до изоморфизма. С другой стороны, сама резольвента однозначно определяется группами
Резольвента определяет спмплпциальное множество Моднозначно с точностью до изоморфизма. С другой стороны, сама резольвента однозначно определяется группами 
 и коциклами
и коциклами  Поэтому резольвентой можно называть также и объект
Поэтому резольвентой можно называть также и объект  состоящий из групп
состоящий из групп  и коциклов
и коциклов  Не всякое симплициальное множество Мобладает резольвентой. Основная теорема теории гомотопич. резольвент утверждает, что симплициальное множество Мтогда и только тогда обладает резольвентой, когда оно изоморфно минимальному симплициальному множеству М (X).нек-рого топологич. пространства X. При этом
Не всякое симплициальное множество Мобладает резольвентой. Основная теорема теории гомотопич. резольвент утверждает, что симплициальное множество Мтогда и только тогда обладает резольвентой, когда оно изоморфно минимальному симплициальному множеству М (X).нек-рого топологич. пространства X. При этом  .
. строится следующим образом. Пусть а - произвольный q-мерный симплекс из
строится следующим образом. Пусть а - произвольный q-мерный симплекс из  . Этот симплекс представляет собой отображение
. Этот симплекс представляет собой отображение  , переводящее все вершины симплекса
, переводящее все вершины симплекса  в точку
в точку  . Поэтому на любой одномерной грани (ребре) симплекса
. Поэтому на любой одномерной грани (ребре) симплекса  оно определяет нек-рый элемент группы
оно определяет нек-рый элемент группы  . Таким образом на
. Таким образом на  возникает нек-рый одномерный коцикл над группой
возникает нек-рый одномерный коцикл над группой  , т. е. q-мерный симплекс из
, т. е. q-мерный симплекс из  ; он будет обозначаться
; он будет обозначаться  . Тем самым получено нек-рое (симплициальное) отображение
. Тем самым получено нек-рое (симплициальное) отображение  . Это отображение является изоморфизмом на
. Это отображение является изоморфизмом на  и эпиморфизмом на
и эпиморфизмом на  . Далее проводится индукция: пусть для нек-рого
. Далее проводится индукция: пусть для нек-рого  уже построено симплицнальное множество
уже построено симплицнальное множество  и симплпцнальное отображение
и симплпцнальное отображение  являющееся изоморфизмом на
являющееся изоморфизмом на  и эпиморфизмом на
и эпиморфизмом на  . Для отображения
. Для отображения  существует обратное справа отображение
существует обратное справа отображение  Пусть
Пусть  - препятствие к распространению этого отображения на
- препятствие к распространению этого отображения на  Препятствие
Препятствие  является
является  -мерным коциклом в
-мерным коциклом в  над группой
над группой  относительно коцикла
относительно коцикла  Для любого
Для любого  -мерного симплекса t из Мсимплекс
-мерного симплекса t из Мсимплекс  сравним с t, и потому определен различающий элемент
сравним с t, и потому определен различающий элемент  (см. Различающая). Пусть
(см. Различающая). Пусть  - произвольный q-мерный симплекс из М. На каждой
- произвольный q-мерный симплекс из М. На каждой  -мерной грани симплекса
-мерной грани симплекса  он определяет некоторый
он определяет некоторый  -мерный симплекс
-мерный симплекс  . Сопоставление этой грани элемента
. Сопоставление этой грани элемента  приводит к некоторой
приводит к некоторой  -мерной коцепи в
-мерной коцепи в  над
над  , то есть к некоторому g-мерному симплексу
, то есть к некоторому g-мерному симплексу  симплициаль-ного множества
симплициаль-ного множества  Пара
Пара 
 принадлежит симплициальному множеству
принадлежит симплициальному множеству 
 Для завершения индукции остается заметить, что построенное отображение
Для завершения индукции остается заметить, что построенное отображение  симплициально, является изоморфизмом на
симплициально, является изоморфизмом на  и эпиморфизмом на
и эпиморфизмом на 
 строится по симплициальному множеству
строится по симплициальному множеству  неоднозначно: имеется произвол в выборе обратных отображений
неоднозначно: имеется произвол в выборе обратных отображений  . Проще всего описать эту неоднозначность, понимая резольвенты в смысле (1). Именно, две такие резольвенты
. Проще всего описать эту неоднозначность, понимая резольвенты в смысле (1). Именно, две такие резольвенты  и
и  тогда и только тогда возникают из одного минимального симплициального множества
тогда и только тогда возникают из одного минимального симплициального множества  , когда они изоморфны как последовательности отображений, т. е. когда для любого
, когда они изоморфны как последовательности отображений, т. е. когда для любого  существует такой изоморфизм
существует такой изоморфизм 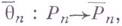 что
что  Чтобы описать этот изоморфизм в терминах резольвент
Чтобы описать этот изоморфизм в терминах резольвент  и
и  , следует заметить, что существование изоморфизма
, следует заметить, что существование изоморфизма  равносильно существованию изоморфизма групп
равносильно существованию изоморфизма групп  При этом
При этом  Далее, для изоморфизма
Далее, для изоморфизма  тогда и только тогда существует следующий изоморфизм
тогда и только тогда существует следующий изоморфизм  когда существует такой
когда существует такой  -изоморфизм
-изоморфизм  (см. Операторный гомоморфизм). и такая коцепь
(см. Операторный гомоморфизм). и такая коцепь 
 что
что 
 определяется формулой
определяется формулой 
 и
и  тогда и только тогда возникают из одного минимального симплициального множества, когда существуют такие изоморфизмы
тогда и только тогда возникают из одного минимального симплициального множества, когда существуют такие изоморфизмы  являющиеся при
являющиеся при  -изоморфизмами, что для любого
-изоморфизмами, что для любого  выполнены соотношения (2), где
выполнены соотношения (2), где  - изоморфизм, последовательно определяемый при
- изоморфизм, последовательно определяемый при  формулой (2'), а при п=1являющийся изоморфизмом, индуцированным изоморфизмом
формулой (2'), а при п=1являющийся изоморфизмом, индуцированным изоморфизмом  . В этом случае резольвенты
. В этом случае резольвенты  и
и  наз. изоморфными. Гомотопической резольвентой пространства Xназ. резольвента симплпциального множества М(Х). Резюмируя, получаем, что два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их гомотопич. резольвенты изоморфны; в частности, два клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда их гомотопические резольвенты изоморфны.
наз. изоморфными. Гомотопической резольвентой пространства Xназ. резольвента симплпциального множества М(Х). Резюмируя, получаем, что два пространства тогда и только тогда слабо гомотопически эквивалентны, когда их гомотопич. резольвенты изоморфны; в частности, два клеточных разбиения тогда и только тогда гомотопически эквивалентны, когда их гомотопические резольвенты изоморфны. , то изоморфизмы
, то изоморфизмы  существуют только при
существуют только при  . В этом случае говорят, что данные резольвенты m-изоморфны. Два клеточных разбиения тогда и только тогда имеют один и тот же re-тип, когда их гомотопич. резольвенты ( п-1)-изоморфны.
. В этом случае говорят, что данные резольвенты m-изоморфны. Два клеточных разбиения тогда и только тогда имеют один и тот же re-тип, когда их гомотопич. резольвенты ( п-1)-изоморфны. , участвующих в их решении. Если рассматриваемое пространство
, участвующих в их решении. Если рассматриваемое пространство  связно, то его резольвента начинается фактически с члена
связно, то его резольвента начинается фактически с члена  . Если решение данной задачи может быть сформулировано лишь с использованием первой нетривиальной группы pn , то эта задача наз. задачей нулевой ступени [напр., задача Хойфа - Уитни о классификации отображений n-мерного полиэдра в
. Если решение данной задачи может быть сформулировано лишь с использованием первой нетривиальной группы pn , то эта задача наз. задачей нулевой ступени [напр., задача Хойфа - Уитни о классификации отображений n-мерного полиэдра в  -связное пространство]. Если для этого требуются группы
-связное пространство]. Если для этого требуются группы  и коцикл
и коцикл  , то задача наз. задачей первой ступени [напр., задача о классификации отображений
, то задача наз. задачей первой ступени [напр., задача о классификации отображений  -мерного полиэдра в
-мерного полиэдра в  -связное пространство]. Аналогично определяются задачи второй, третьей и т. д. ступеней. Известны эффективные решения любых задач нулевой и первой ступеней. Это связано с тем, что для любого
-связное пространство]. Аналогично определяются задачи второй, третьей и т. д. ступеней. Известны эффективные решения любых задач нулевой и первой ступеней. Это связано с тем, что для любого  -связного пространства можно вполне эффективно вычислить класс когомологий коцикла
-связного пространства можно вполне эффективно вычислить класс когомологий коцикла  ; именно, он имеет вид
; именно, он имеет вид  , где
, где  - фундаментальный класс пространства
- фундаментальный класс пространства  а
а  - при
- при  - Стинрода операция, соответствующая естественному спариванию
- Стинрода операция, соответствующая естественному спариванию  а при
а при  - некоторый ее вариант, известный как Понтрягина квадрат. Для задач высших ступеней необходимо аналогичное эффективное вычисление следующих коциклов
- некоторый ее вариант, известный как Понтрягина квадрат. Для задач высших ступеней необходимо аналогичное эффективное вычисление следующих коциклов  ,
, 

 обладает тем свойством, что
обладает тем свойством, что  при
при  . Эта последовательность наз. резольвентой пространства X, если для любого
. Эта последовательность наз. резольвентой пространства X, если для любого  заданы отображения
заданы отображения  индуцирующие изоморфизм гомотопич. групп до размерности пи такие, что
индуцирующие изоморфизм гомотопич. групп до размерности пи такие, что  Эта резольвента с точностью до изоморфизма [понимаемого как изоморфизм последовательностей (см. Последовательностей категория)]определяется однозначно группами
Эта резольвента с точностью до изоморфизма [понимаемого как изоморфизм последовательностей (см. Последовательностей категория)]определяется однозначно группами  и характеристич. классами
и характеристич. классами  расслоений
расслоений  . Резольвента существует для любого линейно связного пространства X[таковой будет, напр., геометрическая реализация "алгебраической" резольвенты (1)] и определяет это пространство с точностью до слабой гомотопич. эквивалентности. Слоем расслоения
. Резольвента существует для любого линейно связного пространства X[таковой будет, напр., геометрическая реализация "алгебраической" резольвенты (1)] и определяет это пространство с точностью до слабой гомотопич. эквивалентности. Слоем расслоения  является пространство типа
является пространство типа  , и в случае, когда Xгомотопически re-просто (см. Гомотопическая группа), напр., односвязно, это расслоение индуцировано из Серра расслоения путей над пространством
, и в случае, когда Xгомотопически re-просто (см. Гомотопическая группа), напр., односвязно, это расслоение индуцировано из Серра расслоения путей над пространством  посредством нек-рого отображения
посредством нек-рого отображения 
 представляющего (см. Эйленберга - Маклейна пространство, Представимый функтор). класс когомологий
представляющего (см. Эйленберга - Маклейна пространство, Представимый функтор). класс когомологий  .
. -связно, то его резольвента фактически начинается с члена
-связно, то его резольвента фактически начинается с члена  При
При  удобно наряду с "абсолютными" резольвентами (3) рассматривать также так наз. резольвенты по модулю простого числа р, определение к-рых отличается от определения резольвент (3) только тем, что гомотопич. группы заменяются их р-компонентами. Если для Xнайдены резольвенты по любому простому модулю р, нахождение "абсолютной" резольвенты, как правило, не представляет труда. Поэтому в задаче вычисления резольвент (включающей задачу вычисления гомотопич. групп) обычно ограничиваются "модульными" резольвентами, в вычислении к-рых могут быть использованы мощные методы теории спектральных последовательностей и теории когомологич. операций. Для нек-рых пространств-вычисление резольвент далеко продвинуто.
удобно наряду с "абсолютными" резольвентами (3) рассматривать также так наз. резольвенты по модулю простого числа р, определение к-рых отличается от определения резольвент (3) только тем, что гомотопич. группы заменяются их р-компонентами. Если для Xнайдены резольвенты по любому простому модулю р, нахождение "абсолютной" резольвенты, как правило, не представляет труда. Поэтому в задаче вычисления резольвент (включающей задачу вычисления гомотопич. групп) обычно ограничиваются "модульными" резольвентами, в вычислении к-рых могут быть использованы мощные методы теории спектральных последовательностей и теории когомологич. операций. Для нек-рых пространств-вычисление резольвент далеко продвинуто. (при пдостаточно большом, чтобы выполнялись условия стационарности) известно уже довольно много первых членов ее резольвенты по модулю 2. Достаточно описать соответствующие группы
(при пдостаточно большом, чтобы выполнялись условия стационарности) известно уже довольно много первых членов ее резольвенты по модулю 2. Достаточно описать соответствующие группы  [то есть 2-компоненты групп
[то есть 2-компоненты групп  ] и классы когомологий
] и классы когомологий  . Первые группы
. Первые группы 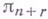 имеют следующий вид
имеют следующий вид 
 имеет вид
имеет вид  где
где 
 - фундаментальный класс. Следующий класс
- фундаментальный класс. Следующий класс  обладает тем свойством, что на слое
обладает тем свойством, что на слое  расслоения
расслоения  он высекает класс
он высекает класс  и однозначно этим свойством характеризуется. Аналогично, класс
и однозначно этим свойством характеризуется. Аналогично, класс 
 однозначно характеризуется тем, что после приведения по модулю 2 он переходит в класс
однозначно характеризуется тем, что после приведения по модулю 2 он переходит в класс  Классы
Классы  и
и  равны нулю, а класс
равны нулю, а класс  однозначно характеризуется тем, что на слое
однозначно характеризуется тем, что на слое  расслоения
расслоения  он высекает класс
он высекает класс  . Наконец, класс
. Наконец, класс  характеризуется тем, что после приведения по модулю 2 он переходит в класс
характеризуется тем, что после приведения по модулю 2 он переходит в класс  .
.