|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОТЕТИЯЗначение ГОМОТЕТИЯ в математической энциклопедии: - преобразование евклидова пространства относительно пек-рой точки О, ставящее в соответствие каждой точке Мточку М', лежащую на прямой ОМ, по правилу где k - постоянное, отличное от нуля число, наз. коэффициентом Г. Точка Оназ. центром Г. При k>0 точки М и М' лежат на одном луче, при k<0 - по разные стороны от центра. Точке Осоответствует сама эта точка. Г. есть частный случай подобия. Две фигуры наз. гомотетичным и (а также подобными и подобно расположенными, или перспективно-подобным и), если каждая состоит из точек, получаемых преобразованием Г. из другой фигуры относительно нек-рого центра Г. Простейшие свойства Г.: Г. есть взаимно однозначное отображение евклидова пространства в себя с одной неподвижной точкой. При k= 1 Г. есть тождественное преобразование. Г. переводит прямую (плоскость), проходящую через центр Г., в себя, прямую (плоскость), не проходящую через центр,- в прямую (плоскость), ей параллельную; углы между прямыми (плоскостями) при Г. сохраняются. Отрезки при Г. переходят в параллельные им отрезки с длиной, уменьшенной или увеличенной в |k| раз, т. е. Г. есть сжатие (растяжение) евклидова пространства к точке О. Всякая сфера при Г. преобразуется в сферу, причем центр одной переходит в центр другой. Г. задается чаще всего (геометрически) центром Г. и парой соответственных точек или двумя парами соответственных точек. Г. есть аффинное преобразование, имеющее одну (и только одну) двойную точку. В га-мерных евклидовых пространствах Г. оставляет инвариантными каждую из совокупностей Аналогично определяется Г. в псевдоевклидовых пространствах. Г. в римановых пространствах и в псевдо-римановых пространствах определяется как преобразование, переводящее метрику пространства в себя с точностью до постоянного множителя. Совокупность Г. составляет группу преобразований Ли, причем r-членная группа Г. риманова пространства содержит |
|
|
|

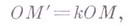

 fe-мерпых плоскостей пространства.
fe-мерпых плоскостей пространства. -членную Нормальную подгруппу движений. И. П. Егоров
-членную Нормальную подгруппу движений. И. П. Егоров