"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОЛОГИЧЕСКОЕ ОПОЯСЫВАНИЕ
Значение ГОМОЛОГИЧЕСКОЕ ОПОЯСЫВАНИЕ в математической энциклопедии:
метод, позволяющий характеризовать размерность компакта, лежащего в евклидовом пространстве  , в терминах метрич. свойств дополнительного пространства. Назовем мерой существенности цикла z компакта
, в терминах метрич. свойств дополнительного пространства. Назовем мерой существенности цикла z компакта  верхнюю грань тех
верхнюю грань тех  , для к-рых можно подобрать такой компактный носитель
, для к-рых можно подобрать такой компактный носитель  цикла z, что цикл не гомологичен нулю в
цикла z, что цикл не гомологичен нулю в  . Назовем р-мерным гомологическим поперечником
. Назовем р-мерным гомологическим поперечником  цикла zоткрытого множества
цикла zоткрытого множества  нижнюю грань р-мерных поперечников тел всех циклов, гомологичных в Г циклу z. Здесь под р-м ерным поперечником
нижнюю грань р-мерных поперечников тел всех циклов, гомологичных в Г циклу z. Здесь под р-м ерным поперечником  компакта
компакта  понимается нижняя грань тех
понимается нижняя грань тех  , для к-рых существует непрерывный
, для к-рых существует непрерывный  -сдвиг компакта. Xв р-мерный компакт (и потому полиэдр).
-сдвиг компакта. Xв р-мерный компакт (и потому полиэдр).
Всякий ( п-1)-мерный цикл открытого множества  , зацепленный с каждой точкой компакта Ф, наз. мешком вокруг компакта Ф.
, зацепленный с каждой точкой компакта Ф, наз. мешком вокруг компакта Ф.
Теорема о мешках. Пусть  Тогда существует такое
Тогда существует такое  , что всякий мешок вокруг компакта Ф имеет (r-1)-мерный гомологич. поперечник, больший
, что всякий мешок вокруг компакта Ф имеет (r-1)-мерный гомологич. поперечник, больший  , тогда как r-мерный гомологич. поперечник любого цикла в Г равен нулю. При этом всегда имеются мешки вокруг Ф со сколь угодно малой мерой существенности. Если же
, тогда как r-мерный гомологич. поперечник любого цикла в Г равен нулю. При этом всегда имеются мешки вокруг Ф со сколь угодно малой мерой существенности. Если же  , то существует такое
, то существует такое  , что для всякого мешка
, что для всякого мешка  вокруг Ф выполняется
вокруг Ф выполняется  (при этом
(при этом  и
и  для всех мешков
для всех мешков  ).
).
Теорема о мешках может быть еще более усилена с помощью понятия пояса вокруг компакта.
Теорема о поясах. Пусть  - компакт размерности r. Существует такое
- компакт размерности r. Существует такое  что для любого
что для любого  и любого
и любого  в
в  имеется
имеется  -мерный цикл v(пояс размерности п - k вокруг Ф), при k>l ограничивающий в Г, для к-рого
-мерный цикл v(пояс размерности п - k вокруг Ф), при k>l ограничивающий в Г, для к-рого  и, кроме того, для всякого цикла w, гомологичного циклу
и, кроме того, для всякого цикла w, гомологичного циклу  в
в  -окрестности последнего относительно Г имеет место
-окрестности последнего относительно Г имеет место  ; для всякой цепи х, ограниченной циклом
; для всякой цепи х, ограниченной циклом  в
в  , имеет место
, имеет место 
С другой стороны, если  и
и  то при любом
то при любом  всякий
всякий  -мерный цикл z в Г, для к-рого
-мерный цикл z в Г, для к-рого  , гомологичен в своей
, гомологичен в своей  -окрестности (относительно Г) нек-рому циклу
-окрестности (относительно Г) нек-рому циклу  со сколь угодно малым
со сколь угодно малым  . Далее, если
. Далее, если  и
и  то при произвольном
то при произвольном  всякий
всякий  -мерный цикл z, ограничивающий в Г, для к-рого
-мерный цикл z, ограничивающий в Г, для к-рого  (и
(и  при
при  -1), ограничивает в Г цепь хс
-1), ограничивает в Г цепь хс 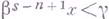 . Здесь через
. Здесь через  ,
,  , обозначена нижняя грань тех
, обозначена нижняя грань тех  , для к-рых существует
, для к-рых существует  -сдвиг вершин цепи х, посредством к-рого цепь хвырождается до размерности р;через ix обозначена нижняя грань тех
-сдвиг вершин цепи х, посредством к-рого цепь хвырождается до размерности р;через ix обозначена нижняя грань тех  , для к-рых существует
, для к-рых существует  -сдвиг вершин х, переводящий хв нулевую цепь.
-сдвиг вершин х, переводящий хв нулевую цепь.
Лит.:[1] Александров П. С., Введение в гомологическую теорию размерности и общую комбинаторную топологию, М., 1975. А. А. Мальцев.

 , в терминах метрич. свойств дополнительного пространства. Назовем мерой существенности цикла z компакта
, в терминах метрич. свойств дополнительного пространства. Назовем мерой существенности цикла z компакта  верхнюю грань тех
верхнюю грань тех  , для к-рых можно подобрать такой компактный носитель
, для к-рых можно подобрать такой компактный носитель  цикла z, что цикл не гомологичен нулю в
цикла z, что цикл не гомологичен нулю в  . Назовем р-мерным гомологическим поперечником
. Назовем р-мерным гомологическим поперечником  цикла zоткрытого множества
цикла zоткрытого множества  нижнюю грань р-мерных поперечников тел всех циклов, гомологичных в Г циклу z. Здесь под р-м ерным поперечником
нижнюю грань р-мерных поперечников тел всех циклов, гомологичных в Г циклу z. Здесь под р-м ерным поперечником  компакта
компакта  понимается нижняя грань тех
понимается нижняя грань тех  , для к-рых существует непрерывный
, для к-рых существует непрерывный  -сдвиг компакта. Xв р-мерный компакт (и потому полиэдр).
-сдвиг компакта. Xв р-мерный компакт (и потому полиэдр). , зацепленный с каждой точкой компакта Ф, наз. мешком вокруг компакта Ф.
, зацепленный с каждой точкой компакта Ф, наз. мешком вокруг компакта Ф. Тогда существует такое
Тогда существует такое  , что всякий мешок вокруг компакта Ф имеет (r-1)-мерный гомологич. поперечник, больший
, что всякий мешок вокруг компакта Ф имеет (r-1)-мерный гомологич. поперечник, больший  , тогда как r-мерный гомологич. поперечник любого цикла в Г равен нулю. При этом всегда имеются мешки вокруг Ф со сколь угодно малой мерой существенности. Если же
, тогда как r-мерный гомологич. поперечник любого цикла в Г равен нулю. При этом всегда имеются мешки вокруг Ф со сколь угодно малой мерой существенности. Если же  , то существует такое
, то существует такое  , что для всякого мешка
, что для всякого мешка  вокруг Ф выполняется
вокруг Ф выполняется  (при этом
(при этом  и
и  для всех мешков
для всех мешков  ).
). - компакт размерности r. Существует такое
- компакт размерности r. Существует такое  что для любого
что для любого  и любого
и любого  в
в  имеется
имеется  -мерный цикл v(пояс размерности п - k вокруг Ф), при k>l ограничивающий в Г, для к-рого
-мерный цикл v(пояс размерности п - k вокруг Ф), при k>l ограничивающий в Г, для к-рого  и, кроме того, для всякого цикла w, гомологичного циклу
и, кроме того, для всякого цикла w, гомологичного циклу  в
в  -окрестности последнего относительно Г имеет место
-окрестности последнего относительно Г имеет место  ; для всякой цепи х, ограниченной циклом
; для всякой цепи х, ограниченной циклом  в
в  , имеет место
, имеет место 
 и
и  то при любом
то при любом  всякий
всякий  -мерный цикл z в Г, для к-рого
-мерный цикл z в Г, для к-рого  , гомологичен в своей
, гомологичен в своей  -окрестности (относительно Г) нек-рому циклу
-окрестности (относительно Г) нек-рому циклу  со сколь угодно малым
со сколь угодно малым  . Далее, если
. Далее, если  и
и  то при произвольном
то при произвольном  всякий
всякий  -мерный цикл z, ограничивающий в Г, для к-рого
-мерный цикл z, ограничивающий в Г, для к-рого  (и
(и  при
при  -1), ограничивает в Г цепь хс
-1), ограничивает в Г цепь хс 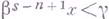 . Здесь через
. Здесь через  ,
,  , обозначена нижняя грань тех
, обозначена нижняя грань тех  , для к-рых существует
, для к-рых существует  -сдвиг вершин цепи х, посредством к-рого цепь хвырождается до размерности р;через ix обозначена нижняя грань тех
-сдвиг вершин цепи х, посредством к-рого цепь хвырождается до размерности р;через ix обозначена нижняя грань тех  , для к-рых существует
, для к-рых существует  -сдвиг вершин х, переводящий хв нулевую цепь.
-сдвиг вершин х, переводящий хв нулевую цепь.