"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОЛОГИЧЕСКАЯ РАЗМЕРНОСТЬ
Значение ГОМОЛОГИЧЕСКАЯ РАЗМЕРНОСТЬ в математической энциклопедии:
пространства Xпо группе коэффициентов G- наибольшее целое число п, при к-ром для нек-рого замкнутого множества  отлична от нуля группа
отлична от нуля группа 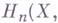
 гомологии Александрова - Чеха. Г. р. обозначается
гомологии Александрова - Чеха. Г. р. обозначается  . Аналогично определяется когомологическая размерность - наименьшее целое n, для которого отображение
. Аналогично определяется когомологическая размерность - наименьшее целое n, для которого отображение  эпиморфно для всех замкнутых
эпиморфно для всех замкнутых  . Под гомологической теорией размерности обычно подразумевается ее когомологический вариант, значительно глубже разработанный. Это объясняется тем что когомологии Александрова - Чеха удовлетворяют всем Стинрода - Эйленберга аксиомам, включая точность и потому применение когомологии оказалось более эффективным. На категории метризуемых компактов, где между группами
. Под гомологической теорией размерности обычно подразумевается ее когомологический вариант, значительно глубже разработанный. Это объясняется тем что когомологии Александрова - Чеха удовлетворяют всем Стинрода - Эйленберга аксиомам, включая точность и потому применение когомологии оказалось более эффективным. На категории метризуемых компактов, где между группами

имеет место Понтрягина двойственность, гомологический подход с коэффициентами в компактной группе G эквивалентен когомологическому подходу с коэффициентами в двойственной группе  ; аналогично, оба подхода эквивалентны, если в качестве коэффициентов берутся элементы одного и того же поля G.
; аналогично, оба подхода эквивалентны, если в качестве коэффициентов берутся элементы одного и того же поля G.
Гомологическая теория размерности берет свое начало с утверждения, полученного П. С. Александровым: соотношение  где dim - лебегова размерность, эквивалентно тому, что любое непрерывное отображение в n-мерную сферу Sn произвольного замкнутого множества
где dim - лебегова размерность, эквивалентно тому, что любое непрерывное отображение в n-мерную сферу Sn произвольного замкнутого множества  может быть продолжено до отображения в
может быть продолжено до отображения в  всего X. Отсюда было получено, что dim
всего X. Отсюда было получено, что dim , если dim
, если dim  , a Zесть группа целых чисел. Затем Л. С. Понтрягиным было замечено, что Г. р. по разным областям коэффициентов не совпадают (вообще же, как это вытекает из формул универсальных коэффициентов,
, a Zесть группа целых чисел. Затем Л. С. Понтрягиным было замечено, что Г. р. по разным областям коэффициентов не совпадают (вообще же, как это вытекает из формул универсальных коэффициентов,  для любого компакта X);таким образом, Г. р. являются вместе с лебеговой размерностью нек-рыми топологич. инвариантами пространства X.
для любого компакта X);таким образом, Г. р. являются вместе с лебеговой размерностью нек-рыми топологич. инвариантами пространства X.
Г. р.  обладает многими свойствами обычной размерности dim. Именно, если А - замкнутое подмножество из X, то
обладает многими свойствами обычной размерности dim. Именно, если А - замкнутое подмножество из X, то  где каждое Xзамкнуто в X, то
где каждое Xзамкнуто в X, то

и т. п. Справедлива теорема Александрова о препятствии: подмножества евклидова пространства  , имеющие Г. р. г, (локально) зацепляются
, имеющие Г. р. г, (локально) зацепляются  -мерными циклами. См. также Размерность. Центральное место в гомологич. размерности занимают исследования соотношений между Г. р. по различным областям коэффициентов. Возникающие в этом направлении задачи имеют много непосредственных приложений в теории размерности и тесно переплетаются с нек-рыми важнейшими задачами теории групп преобразований. Большую роль играет анализ размерности произведения; напр.,
-мерными циклами. См. также Размерность. Центральное место в гомологич. размерности занимают исследования соотношений между Г. р. по различным областям коэффициентов. Возникающие в этом направлении задачи имеют много непосредственных приложений в теории размерности и тесно переплетаются с нек-рыми важнейшими задачами теории групп преобразований. Большую роль играет анализ размерности произведения; напр.,
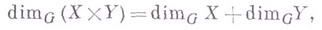
если G - поле рациональных чисел или поле вычетов по простому модулю, а

ля любого компакта  тогда и только
тогда и только  тогда, когда все размерности
тогда, когда все размерности  совпадают.
совпадают.
Внешний облик гомологич. теории размерности существенно изменился в связи с применением аппарата пучков теории, получила самостоятельное развитие когомологич. теория размерности с коэффициентами в пучках (основное определение такое же). Новые методы оказались применимыми к решению ряда задач, связанных с поведением размерности при непрерывных отображениях, а также позволили расширить область применимости теории до категории паракомпактных пространств.
Лит:[1] Гуревич В., Волмэн Г., Теория размерности пер. с англ., М., 1948; [2] Кузьмине в В. И., "Успехи матем. наук", 1968, т. 23, в. 5(143), о. 3-49.

 отлична от нуля группа
отлична от нуля группа 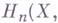
 гомологии Александрова - Чеха. Г. р. обозначается
гомологии Александрова - Чеха. Г. р. обозначается  . Аналогично определяется когомологическая размерность - наименьшее целое n, для которого отображение
. Аналогично определяется когомологическая размерность - наименьшее целое n, для которого отображение  эпиморфно для всех замкнутых
эпиморфно для всех замкнутых  . Под гомологической теорией размерности обычно подразумевается ее когомологический вариант, значительно глубже разработанный. Это объясняется тем что когомологии Александрова - Чеха удовлетворяют всем Стинрода - Эйленберга аксиомам, включая точность и потому применение когомологии оказалось более эффективным. На категории метризуемых компактов, где между группами
. Под гомологической теорией размерности обычно подразумевается ее когомологический вариант, значительно глубже разработанный. Это объясняется тем что когомологии Александрова - Чеха удовлетворяют всем Стинрода - Эйленберга аксиомам, включая точность и потому применение когомологии оказалось более эффективным. На категории метризуемых компактов, где между группами
 ; аналогично, оба подхода эквивалентны, если в качестве коэффициентов берутся элементы одного и того же поля G.
; аналогично, оба подхода эквивалентны, если в качестве коэффициентов берутся элементы одного и того же поля G. где dim - лебегова размерность, эквивалентно тому, что любое непрерывное отображение в n-мерную сферу Sn произвольного замкнутого множества
где dim - лебегова размерность, эквивалентно тому, что любое непрерывное отображение в n-мерную сферу Sn произвольного замкнутого множества  может быть продолжено до отображения в
может быть продолжено до отображения в  всего X. Отсюда было получено, что dim
всего X. Отсюда было получено, что dim , если dim
, если dim  , a Zесть группа целых чисел. Затем Л. С. Понтрягиным было замечено, что Г. р. по разным областям коэффициентов не совпадают (вообще же, как это вытекает из формул универсальных коэффициентов,
, a Zесть группа целых чисел. Затем Л. С. Понтрягиным было замечено, что Г. р. по разным областям коэффициентов не совпадают (вообще же, как это вытекает из формул универсальных коэффициентов,  для любого компакта X);таким образом, Г. р. являются вместе с лебеговой размерностью нек-рыми топологич. инвариантами пространства X.
для любого компакта X);таким образом, Г. р. являются вместе с лебеговой размерностью нек-рыми топологич. инвариантами пространства X. обладает многими свойствами обычной размерности dim. Именно, если А - замкнутое подмножество из X, то
обладает многими свойствами обычной размерности dim. Именно, если А - замкнутое подмножество из X, то  где каждое Xзамкнуто в X, то
где каждое Xзамкнуто в X, то 
 , имеющие Г. р. г, (локально) зацепляются
, имеющие Г. р. г, (локально) зацепляются  -мерными циклами. См. также Размерность. Центральное место в гомологич. размерности занимают исследования соотношений между Г. р. по различным областям коэффициентов. Возникающие в этом направлении задачи имеют много непосредственных приложений в теории размерности и тесно переплетаются с нек-рыми важнейшими задачами теории групп преобразований. Большую роль играет анализ размерности произведения; напр.,
-мерными циклами. См. также Размерность. Центральное место в гомологич. размерности занимают исследования соотношений между Г. р. по различным областям коэффициентов. Возникающие в этом направлении задачи имеют много непосредственных приложений в теории размерности и тесно переплетаются с нек-рыми важнейшими задачами теории групп преобразований. Большую роль играет анализ размерности произведения; напр.,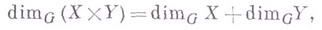

 тогда и только
тогда и только  тогда, когда все размерности
тогда, когда все размерности  совпадают.
совпадают.