"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОЛОГИИ КОМПЛЕКСАЗначение ГОМОЛОГИИ КОМПЛЕКСА в математической энциклопедии:
исходное понятие для различных гомологич. конструкций. Пусть А - абелева категория и  - цепной комплекс в категории А, т. е. семейство объектов - цепной комплекс в категории А, т. е. семейство объектов  категории Аи таких морфизмов категории Аи таких морфизмов  что что  для всех для всех  . Факторобъекты . Факторобъекты  наз. n-ми гомологиями комплекса К. и обозначаются наз. n-ми гомологиями комплекса К. и обозначаются  . Семейство . Семейство  обозначается также через обозначается также через  . Понятие Г. к. является основой для ряда важных конструкций в гомологич. алгебре, коммутативной алгебре, ал-гебраич. геометрии, топологии. Так, в топологии каждое топологич. пространство Xопределяет цепной комплекс в категории . Понятие Г. к. является основой для ряда важных конструкций в гомологич. алгебре, коммутативной алгебре, ал-гебраич. геометрии, топологии. Так, в топологии каждое топологич. пространство Xопределяет цепной комплекс в категории 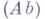 абелевых групп: абелевых групп: Здесь Здесь  - группа n-мерных сингулярных цепей пространства X, а - группа n-мерных сингулярных цепей пространства X, а  - граничный гомоморфизм, п-eгомологии этого комплекса наз. n-ми группами сингулярных гомологии пространства Xи обозначаются - граничный гомоморфизм, п-eгомологии этого комплекса наз. n-ми группами сингулярных гомологии пространства Xи обозначаются  . Двойственным образом определяется понятие когомологии коцепного комплекса. . Двойственным образом определяется понятие когомологии коцепного комплекса.
Лит.:[1] Маклейн С., Гомология, пер. с англ., М., 1966. И. В. Долгачев.
|

 - цепной комплекс в категории А, т. е. семейство объектов
- цепной комплекс в категории А, т. е. семейство объектов  категории Аи таких морфизмов
категории Аи таких морфизмов  что
что  для всех
для всех  . Факторобъекты
. Факторобъекты  наз. n-ми гомологиями комплекса К. и обозначаются
наз. n-ми гомологиями комплекса К. и обозначаются  . Семейство
. Семейство  обозначается также через
обозначается также через  . Понятие Г. к. является основой для ряда важных конструкций в гомологич. алгебре, коммутативной алгебре, ал-гебраич. геометрии, топологии. Так, в топологии каждое топологич. пространство Xопределяет цепной комплекс в категории
. Понятие Г. к. является основой для ряда важных конструкций в гомологич. алгебре, коммутативной алгебре, ал-гебраич. геометрии, топологии. Так, в топологии каждое топологич. пространство Xопределяет цепной комплекс в категории 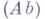 абелевых групп:
абелевых групп: Здесь
Здесь  - группа n-мерных сингулярных цепей пространства X, а
- группа n-мерных сингулярных цепей пространства X, а  - граничный гомоморфизм, п-eгомологии этого комплекса наз. n-ми группами сингулярных гомологии пространства Xи обозначаются
- граничный гомоморфизм, п-eгомологии этого комплекса наз. n-ми группами сингулярных гомологии пространства Xи обозначаются  . Двойственным образом определяется понятие когомологии коцепного комплекса.
. Двойственным образом определяется понятие когомологии коцепного комплекса.