|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОМОЛОГИИ ДИНАМИЧЕСКОЙ СИСТЕМЫЗначение ГОМОЛОГИИ ДИНАМИЧЕСКОЙ СИСТЕМЫ в математической энциклопедии: когомологии динамической системы,- один из инвариантов в эргодической теории, построение к-рого напоминает построение когомологии группы (см. [1]). В простейшем случае одномерных (ко)гомологий Пока (к 1977) Г. д. с. не вычислены ни в одном нетривиальном примере. Использование "гомологических" понятий в эргодич. теории определяется тем, что в различных конкретных случаях бывает важно знать (и иногда действительно удается выяснить), является ли та или иная определенная функция кограницей. Лит.:[1] Кириллов А. А., "Успехи матем. наук", 1967, т. 22, № 5, с. 67-80; [2] Степин А. М., "Функциональн. анализ и его приложения", 1971, т. 5, .№ 2, с. 91-2. Д. В. Аносов. |
|
|
|

 каскада, получающегося итерированием автоморфизма Тпространства с мерой X, определение эквивалентно следующему. Пусть
каскада, получающегося итерированием автоморфизма Тпространства с мерой X, определение эквивалентно следующему. Пусть  - группа по сложению всех измеримых функций на X(соответственно группа по умножению измеримых функций f, для к-рых
- группа по сложению всех измеримых функций на X(соответственно группа по умножению измеримых функций f, для к-рых  почти всюду). Аддитивной (соответственно мультипликативной) (ко) границей функции
почти всюду). Аддитивной (соответственно мультипликативной) (ко) границей функции  наз. функция
наз. функция 
 (соответственно
(соответственно  ). Обозначая совокупность всех (ко)границ через
). Обозначая совокупность всех (ко)границ через  , можно определить аддитивную (соответственно мультипликативную) группу (ко)гомологий
, можно определить аддитивную (соответственно мультипликативную) группу (ко)гомологий  как факторгруппу
как факторгруппу 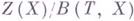 . Вместо всех измеримых функций могут рассматриваться и более узкие классы функций. Г. д. с. являются инвариантами траекторного изоморфизма (подробности для
. Вместо всех измеримых функций могут рассматриваться и более узкие классы функций. Г. д. с. являются инвариантами траекторного изоморфизма (подробности для  см. в [2]).
см. в [2]).