"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГОЛОМОРФНОЕ ОТОБРАЖЕНИЕ
Значение ГОЛОМОРФНОЕ ОТОБРАЖЕНИЕ в математической энциклопедии:
отображение 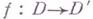 области
области  в область
в область  , при к-ром
, при к-ром
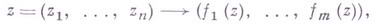
где все координатные функции  голоморфны в D. При
голоморфны в D. При  Г. о. совпадает с голоморфной функцией (см. Аналитическая функция).
Г. о. совпадает с голоморфной функцией (см. Аналитическая функция).
Г. о. f наз. невырожденным в точке 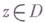 , если ранг якобиевой матрицы
, если ранг якобиевой матрицы 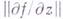 в точке z максимален (
в точке z максимален (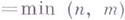 ). Г. о. наз. невырожденным в области D, если оно невырождено во всех точках
). Г. о. наз. невырожденным в области D, если оно невырождено во всех точках  . При m=n невырожденность f эквивалентна условию
. При m=n невырожденность f эквивалентна условию
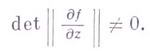
При 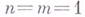 невырожденное Г. о. есть конформное отображение. При
невырожденное Г. о. есть конформное отображение. При 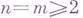 невырожденное Г. о., вообще говоря, не сохраняет углов между направлениями. Если Г. о. f невырождено в точке
невырожденное Г. о., вообще говоря, не сохраняет углов между направлениями. Если Г. о. f невырождено в точке 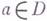 и
и  , то f локально обратимо, т. е. существуют окрестности
, то f локально обратимо, т. е. существуют окрестности 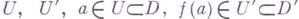 и Г. о.
и Г. о.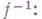
 такие, что
такие, что 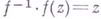 для всех
для всех 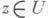 . Если Г. о. f взаимно однозначно отображает Dна f(D).и т=п, то f невырождено в D;при m>n это неверно, напр.
. Если Г. о. f взаимно однозначно отображает Dна f(D).и т=п, то f невырождено в D;при m>n это неверно, напр. 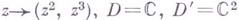 . Если
. Если  и f невырождено
и f невырождено
в D, то образ области D тоже является областью в С m; прп m>1 принцип сохранения области не выполняется для отображений, вырожденных в нек-рых точках, напр. 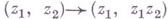 ,
,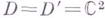
Если 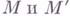 - комплексные многообразия,
- комплексные многообразия,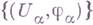 и
и 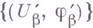 - атласы их локальных систем координат
- атласы их локальных систем координат 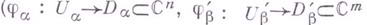 - гомеоморфизмы; см. Многообразие), то отображение
- гомеоморфизмы; см. Многообразие), то отображение 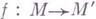 наз. голоморфным, если
наз. голоморфным, если 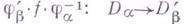 есть Г. о. для всех
есть Г. о. для всех 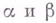 . Аналогично определяются Г. о. комплексных пространств (см. Аналитическое отображение). См. также Виголоморфное отображение.
. Аналогично определяются Г. о. комплексных пространств (см. Аналитическое отображение). См. также Виголоморфное отображение.
Лит.:[1] Ганнинг Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969. Е. Д. Соломенцее, Е. М. Чирка.

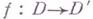 области
области  в область
в область  , при к-ром
, при к-ром 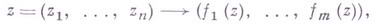
 голоморфны в D. При
голоморфны в D. При  Г. о. совпадает с голоморфной функцией (см. Аналитическая функция).
Г. о. совпадает с голоморфной функцией (см. Аналитическая функция).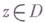 , если ранг якобиевой матрицы
, если ранг якобиевой матрицы 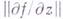 в точке z максимален (
в точке z максимален (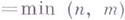 ). Г. о. наз. невырожденным в области D, если оно невырождено во всех точках
). Г. о. наз. невырожденным в области D, если оно невырождено во всех точках  . При m=n невырожденность f эквивалентна условию
. При m=n невырожденность f эквивалентна условию 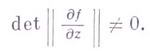
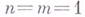 невырожденное Г. о. есть конформное отображение. При
невырожденное Г. о. есть конформное отображение. При 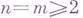 невырожденное Г. о., вообще говоря, не сохраняет углов между направлениями. Если Г. о. f невырождено в точке
невырожденное Г. о., вообще говоря, не сохраняет углов между направлениями. Если Г. о. f невырождено в точке 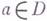 и
и  , то f локально обратимо, т. е. существуют окрестности
, то f локально обратимо, т. е. существуют окрестности 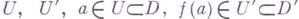 и Г. о.
и Г. о.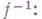
 такие, что
такие, что 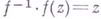 для всех
для всех 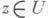 . Если Г. о. f взаимно однозначно отображает Dна f(D).и т=п, то f невырождено в D;при m>n это неверно, напр.
. Если Г. о. f взаимно однозначно отображает Dна f(D).и т=п, то f невырождено в D;при m>n это неверно, напр. 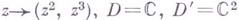 . Если
. Если  и f невырождено
и f невырождено 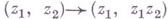 ,
,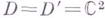
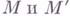 - комплексные многообразия,
- комплексные многообразия,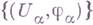 и
и 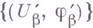 - атласы их локальных систем координат
- атласы их локальных систем координат 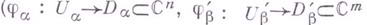 - гомеоморфизмы; см. Многообразие), то отображение
- гомеоморфизмы; см. Многообразие), то отображение 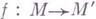 наз. голоморфным, если
наз. голоморфным, если 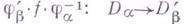 есть Г. о. для всех
есть Г. о. для всех 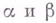 . Аналогично определяются Г. о. комплексных пространств (см. Аналитическое отображение). См. также Виголоморфное отображение.
. Аналогично определяются Г. о. комплексных пространств (см. Аналитическое отображение). См. также Виголоморфное отображение.