"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЛОБАЛЬНО СИММЕТРИЧЕСКОЕ РИМАНОВО ПРОСТРАНСТВО
Значение ГЛОБАЛЬНО СИММЕТРИЧЕСКОЕ РИМАНОВО ПРОСТРАНСТВО в математической энциклопедии:
- риманово многообразие М, каждая точка рк-рого является изолированной неподвижной точкой нек-рой ннволютивной нзометрии Sp многообразия М, т. е.  есть тождественное преобразование. Пусть G - компонента единицы группы изометрий пространства Ми К - стационарная подгруппа точки р. Тогда Мявляется однородным пространством
есть тождественное преобразование. Пусть G - компонента единицы группы изометрий пространства Ми К - стационарная подгруппа точки р. Тогда Мявляется однородным пространством , и отображение
, и отображение  есть инволютивный автоморфизм группы G, причем Ксодержится в замкнутой подгруппе
есть инволютивный автоморфизм группы G, причем Ксодержится в замкнутой подгруппе  всех неподвижных точек автоморфизма Ф и содержит компоненту единицы группы
всех неподвижных точек автоморфизма Ф и содержит компоненту единицы группы  .
.
Пусть  - вещественная алгебра Ли,
- вещественная алгебра Ли,  - ее инво-лютнвный автоморфизм и k - подалгебра в g, состоящая из всех
- ее инво-лютнвный автоморфизм и k - подалгебра в g, состоящая из всех  -неподвижных элементов. Рассмотрим связную подгруппу Кприсоединенной группы
-неподвижных элементов. Рассмотрим связную подгруппу Кприсоединенной группы  , соответствующую подалгебре k. Если группа Ккомпактна, то kназ. компактно вложенной подалгеброй алгебры
, соответствующую подалгебре k. Если группа Ккомпактна, то kназ. компактно вложенной подалгеброй алгебры  , а пара
, а пара  наз. ортогональной симметрической алгеброй Ли. Пусть g=k+m - разложение на собственные подпространства автоморфизма
наз. ортогональной симметрической алгеброй Ли. Пусть g=k+m - разложение на собственные подпространства автоморфизма 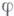 , отвечающие собственным значениям 1 и -1. Пара (
, отвечающие собственным значениям 1 и -1. Пара ( ) наз.: а) алгеброй компактного типа, если gкомпактна и полупроста; б) алгеброй некомпактного типа, если g=k+m есть Картана разложение;в) алгеброй евклидова типа, если m - абелев идеал в g. Пусть (
) наз.: а) алгеброй компактного типа, если gкомпактна и полупроста; б) алгеброй некомпактного типа, если g=k+m есть Картана разложение;в) алгеброй евклидова типа, если m - абелев идеал в g. Пусть ( ) - ортогональная симметрия, алгебра Ли и g=k+m - указанное разложение. Обозначим через
) - ортогональная симметрия, алгебра Ли и g=k+m - указанное разложение. Обозначим через  подмножество k+im комплексной оболочки
подмножество k+im комплексной оболочки  алгебры g. Отображение
алгебры g. Отображение

есть инволютивный автоморфизм алгебры  и (
и ( ) есть ортогональная симметрич. алгебра Ли, к-рая наз. двойственной к алгебре (
) есть ортогональная симметрич. алгебра Ли, к-рая наз. двойственной к алгебре ( ). Если (
). Если ( ) - алгебра компактного типа, то (
) - алгебра компактного типа, то ( ) - алгебра некомпактного типа, и наоборот.
) - алгебра некомпактного типа, и наоборот.
Каждое Г. с. р. п.  порождает ортогональную симметрич. алгебру Ли (
порождает ортогональную симметрич. алгебру Ли ( ), где g - алгебра Ли группы G, а
), где g - алгебра Ли группы G, а  ( е - единица группы).
( е - единица группы).  наз. пространством компактного или некомпактного типа в соответствии с типом порождаемой им пары (
наз. пространством компактного или некомпактного типа в соответствии с типом порождаемой им пары (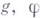 ). Каждое односвязное Г. с. р. п. Мявляется прямым произведением:
). Каждое односвязное Г. с. р. п. Мявляется прямым произведением: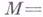
 где
где  - евклидово пространство,
- евклидово пространство,  и
и  - Г. с. р. п. компактного и некомпактного типа соответственно. Для всякого пространства некомпактного типа кривизна в любом двумерном направлении неположительна, а для пространств компактного типа такая кривизна всюду неотрицательна. Любое пространство некомпактного типа диффеоморфно евклидову пространству.
- Г. с. р. п. компактного и некомпактного типа соответственно. Для всякого пространства некомпактного типа кривизна в любом двумерном направлении неположительна, а для пространств компактного типа такая кривизна всюду неотрицательна. Любое пространство некомпактного типа диффеоморфно евклидову пространству.
Пусть  - Г. с. р. п. компактного или некомпактного типа. Рангом lпространства Мназ. максимальная размерность плоского вполне геодезич. подмногообразия в М. Пусть
- Г. с. р. п. компактного или некомпактного типа. Рангом lпространства Мназ. максимальная размерность плоского вполне геодезич. подмногообразия в М. Пусть  - два плоских вполне геодезич. подмногообразия пространства Мразмерности
- два плоских вполне геодезич. подмногообразия пространства Мразмерности  и X - касательный вектор к Мв точке q. Тогда: 1) существует такой элемент
и X - касательный вектор к Мв точке q. Тогда: 1) существует такой элемент  что
что  и
и  ; 2) существует такой элемент
; 2) существует такой элемент  , что
, что  и
и  - касательный вектор к Ав точке q.
- касательный вектор к Ав точке q.
Пусть  - ортогональная симметрич. алгебра Ли, a kи т - собственные подпространства автоморфизма
- ортогональная симметрич. алгебра Ли, a kи т - собственные подпространства автоморфизма  , отвечающие собственным значениям 1 и - 1. Алгебра
, отвечающие собственным значениям 1 и - 1. Алгебра  наз. неприводимой, если выполняются условия: 1) gполупроста и kне содержит ненулевых идеалов алгебры g;2) алгебра
наз. неприводимой, если выполняются условия: 1) gполупроста и kне содержит ненулевых идеалов алгебры g;2) алгебра  неприводимым образом действует на т. Г. с. р. п. G/K наз. неприводимым, если порождаемая им ортогональная симметрич. алгебра Ли
неприводимым образом действует на т. Г. с. р. п. G/K наз. неприводимым, если порождаемая им ортогональная симметрич. алгебра Ли  неприводима. Две ортогональные симметрич. алгебры Ли
неприводима. Две ортогональные симметрич. алгебры Ли  и
и  наз. изоморфными, если существует такой изоморфизм
наз. изоморфными, если существует такой изоморфизм  алгебры
алгебры  на
на  , что
, что  . Классификация односвязных неприводимых Г. с. р. п. с точностью до пзометрии эквивалентна классификации неприводимых ортогональных симметрич. алгебр Ли с точностью до изоморфизма.
. Классификация односвязных неприводимых Г. с. р. п. с точностью до пзометрии эквивалентна классификации неприводимых ортогональных симметрич. алгебр Ли с точностью до изоморфизма.
Неприводимые ортогональные симметрич. алгебры Ли компактного типа суть: I.  , где
, где  - компактная простая алгебра Ли и
- компактная простая алгебра Ли и  - любой ее инволютивный автоморфизм; II. (
- любой ее инволютивный автоморфизм; II. ( ), где компактная алгебра gявляется прямой суммой двух простых идеалов, к-рые переставляются при помощи автоморфизма
), где компактная алгебра gявляется прямой суммой двух простых идеалов, к-рые переставляются при помощи автоморфизма  .
.
Неприводимые ортогональные симметрич. алгебры Ли некомпактного типа суть: III. ( ), где g - простая некомпактная алгебра Ли над
), где g - простая некомпактная алгебра Ли над  , комплексная оболочка
, комплексная оболочка  к-рой является простой алгеброй Ли над
к-рой является простой алгеброй Ли над  , а
, а  - такой инволютивный автоморфизм алгебры
- такой инволютивный автоморфизм алгебры  , что его неподвижные точки составляют максимальную компактно вложенную подалгебру; IV. (
, что его неподвижные точки составляют максимальную компактно вложенную подалгебру; IV. ( ), где
), где  - простая алгебра Ли над
- простая алгебра Ли над  , рассматриваемая как вещественная алгебра Ли, а
, рассматриваемая как вещественная алгебра Ли, а  - сопряжение алгебры gпо отношению к максимальной компактно вложенной подалгебре k, т. е. отображение
- сопряжение алгебры gпо отношению к максимальной компактно вложенной подалгебре k, т. е. отображение 
 Кроме того, если обозначить через
Кроме того, если обозначить через  алгебру, двойственную к (g,j), то (g,j) типа III и IV, если
алгебру, двойственную к (g,j), то (g,j) типа III и IV, если  типа I и II соответственно, и наоборот.
типа I и II соответственно, и наоборот.
С каждой неприводимой ортогональной симметрич. алгеброй некомпактного типа связано в точности одно Г. с. р. п., причем это пространство односвязно. Для компактных алгебр решение соответствующей задачи значительно сложнее. Достаточно рассмотреть типы I и II. Г. с. р. п., связанные с алгебрами типа II,- это в точности компактные связные простые группы Ли, снабженные римановой структурой, инвариантной относительно левых и правых сдвигов. Задача классификации Г. с. р. п., связанных с алгебрами типа I, с точностью до локальных изометрий равносильна задаче классификации инволютивных автоморфизмов простых компактных алгебр Ли. Глобальная классификация симметрических римановых пространств, связанных с данной ортогональной симметрич. алгеброй  компактного типа, решается следующей теоремой.
компактного типа, решается следующей теоремой.
Пусть  - ортогональная симметрич. алгебра компактного типа, причем подалгебра k неподвижных точек автоморфизма
- ортогональная симметрич. алгебра компактного типа, причем подалгебра k неподвижных точек автоморфизма  не содержит идеалов алгебры g, отличных от
не содержит идеалов алгебры g, отличных от  . Пусть
. Пусть  - односвязная группа Ли с алгеброй Ли
- односвязная группа Ли с алгеброй Ли  - центр группы
- центр группы  - такой автоморфизм группы
- такой автоморфизм группы  , что
, что  и
и 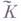 - множество всех неподвижных точек автоморфизма Ф. Для произвольной подгруппы Sгруппы
- множество всех неподвижных точек автоморфизма Ф. Для произвольной подгруппы Sгруппы  положим
положим 
 Г. с. р. п. М, связанные с
Г. с. р. п. М, связанные с  , совпадают с пространствами вида
, совпадают с пространствами вида  где
где 
 снабженными любой G-инвариантной метрикой. Здесь Sпробегает все подгруппы группы
снабженными любой G-инвариантной метрикой. Здесь Sпробегает все подгруппы группы  , а
, а  пробегает все такие подгруппы в
пробегает все такие подгруппы в  что
что 
Лит.: [1] Хелгасон С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [2] Loos О., Symmetric spaces, v. 1-2, N.Y.- Amst., 1969.
А. С. Феденко.

 есть тождественное преобразование. Пусть G - компонента единицы группы изометрий пространства Ми К - стационарная подгруппа точки р. Тогда Мявляется однородным пространством
есть тождественное преобразование. Пусть G - компонента единицы группы изометрий пространства Ми К - стационарная подгруппа точки р. Тогда Мявляется однородным пространством , и отображение
, и отображение  есть инволютивный автоморфизм группы G, причем Ксодержится в замкнутой подгруппе
есть инволютивный автоморфизм группы G, причем Ксодержится в замкнутой подгруппе  всех неподвижных точек автоморфизма Ф и содержит компоненту единицы группы
всех неподвижных точек автоморфизма Ф и содержит компоненту единицы группы  .
. - вещественная алгебра Ли,
- вещественная алгебра Ли,  - ее инво-лютнвный автоморфизм и k - подалгебра в g, состоящая из всех
- ее инво-лютнвный автоморфизм и k - подалгебра в g, состоящая из всех  -неподвижных элементов. Рассмотрим связную подгруппу Кприсоединенной группы
-неподвижных элементов. Рассмотрим связную подгруппу Кприсоединенной группы  , соответствующую подалгебре k. Если группа Ккомпактна, то kназ. компактно вложенной подалгеброй алгебры
, соответствующую подалгебре k. Если группа Ккомпактна, то kназ. компактно вложенной подалгеброй алгебры  , а пара
, а пара  наз. ортогональной симметрической алгеброй Ли. Пусть g=k+m - разложение на собственные подпространства автоморфизма
наз. ортогональной симметрической алгеброй Ли. Пусть g=k+m - разложение на собственные подпространства автоморфизма 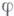 , отвечающие собственным значениям 1 и -1. Пара (
, отвечающие собственным значениям 1 и -1. Пара ( ) наз.: а) алгеброй компактного типа, если gкомпактна и полупроста; б) алгеброй некомпактного типа, если g=k+m есть Картана разложение;в) алгеброй евклидова типа, если m - абелев идеал в g. Пусть (
) наз.: а) алгеброй компактного типа, если gкомпактна и полупроста; б) алгеброй некомпактного типа, если g=k+m есть Картана разложение;в) алгеброй евклидова типа, если m - абелев идеал в g. Пусть ( ) - ортогональная симметрия, алгебра Ли и g=k+m - указанное разложение. Обозначим через
) - ортогональная симметрия, алгебра Ли и g=k+m - указанное разложение. Обозначим через  подмножество k+im комплексной оболочки
подмножество k+im комплексной оболочки  алгебры g. Отображение
алгебры g. Отображение 
 и (
и ( ) есть ортогональная симметрич. алгебра Ли, к-рая наз. двойственной к алгебре (
) есть ортогональная симметрич. алгебра Ли, к-рая наз. двойственной к алгебре ( ). Если (
). Если ( ) - алгебра компактного типа, то (
) - алгебра компактного типа, то ( ) - алгебра некомпактного типа, и наоборот.
) - алгебра некомпактного типа, и наоборот. порождает ортогональную симметрич. алгебру Ли (
порождает ортогональную симметрич. алгебру Ли ( ), где g - алгебра Ли группы G, а
), где g - алгебра Ли группы G, а  ( е - единица группы).
( е - единица группы).  наз. пространством компактного или некомпактного типа в соответствии с типом порождаемой им пары (
наз. пространством компактного или некомпактного типа в соответствии с типом порождаемой им пары (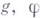 ). Каждое односвязное Г. с. р. п. Мявляется прямым произведением:
). Каждое односвязное Г. с. р. п. Мявляется прямым произведением: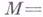
 где
где  - евклидово пространство,
- евклидово пространство,  и
и  - Г. с. р. п. компактного и некомпактного типа соответственно. Для всякого пространства некомпактного типа кривизна в любом двумерном направлении неположительна, а для пространств компактного типа такая кривизна всюду неотрицательна. Любое пространство некомпактного типа диффеоморфно евклидову пространству.
- Г. с. р. п. компактного и некомпактного типа соответственно. Для всякого пространства некомпактного типа кривизна в любом двумерном направлении неположительна, а для пространств компактного типа такая кривизна всюду неотрицательна. Любое пространство некомпактного типа диффеоморфно евклидову пространству. - Г. с. р. п. компактного или некомпактного типа. Рангом lпространства Мназ. максимальная размерность плоского вполне геодезич. подмногообразия в М. Пусть
- Г. с. р. п. компактного или некомпактного типа. Рангом lпространства Мназ. максимальная размерность плоского вполне геодезич. подмногообразия в М. Пусть  - два плоских вполне геодезич. подмногообразия пространства Мразмерности
- два плоских вполне геодезич. подмногообразия пространства Мразмерности  и X - касательный вектор к Мв точке q. Тогда: 1) существует такой элемент
и X - касательный вектор к Мв точке q. Тогда: 1) существует такой элемент  что
что  и
и  ; 2) существует такой элемент
; 2) существует такой элемент  , что
, что  и
и  - касательный вектор к Ав точке q.
- касательный вектор к Ав точке q. - ортогональная симметрич. алгебра Ли, a kи т - собственные подпространства автоморфизма
- ортогональная симметрич. алгебра Ли, a kи т - собственные подпространства автоморфизма  , отвечающие собственным значениям 1 и - 1. Алгебра
, отвечающие собственным значениям 1 и - 1. Алгебра  наз. неприводимой, если выполняются условия: 1) gполупроста и kне содержит ненулевых идеалов алгебры g;2) алгебра
наз. неприводимой, если выполняются условия: 1) gполупроста и kне содержит ненулевых идеалов алгебры g;2) алгебра  неприводимым образом действует на т. Г. с. р. п. G/K наз. неприводимым, если порождаемая им ортогональная симметрич. алгебра Ли
неприводимым образом действует на т. Г. с. р. п. G/K наз. неприводимым, если порождаемая им ортогональная симметрич. алгебра Ли  неприводима. Две ортогональные симметрич. алгебры Ли
неприводима. Две ортогональные симметрич. алгебры Ли  и
и  наз. изоморфными, если существует такой изоморфизм
наз. изоморфными, если существует такой изоморфизм  алгебры
алгебры  на
на  , что
, что  . Классификация односвязных неприводимых Г. с. р. п. с точностью до пзометрии эквивалентна классификации неприводимых ортогональных симметрич. алгебр Ли с точностью до изоморфизма.
. Классификация односвязных неприводимых Г. с. р. п. с точностью до пзометрии эквивалентна классификации неприводимых ортогональных симметрич. алгебр Ли с точностью до изоморфизма. , где
, где  - компактная простая алгебра Ли и
- компактная простая алгебра Ли и  - любой ее инволютивный автоморфизм; II. (
- любой ее инволютивный автоморфизм; II. ( ), где компактная алгебра gявляется прямой суммой двух простых идеалов, к-рые переставляются при помощи автоморфизма
), где компактная алгебра gявляется прямой суммой двух простых идеалов, к-рые переставляются при помощи автоморфизма  .
. ), где g - простая некомпактная алгебра Ли над
), где g - простая некомпактная алгебра Ли над  , комплексная оболочка
, комплексная оболочка  к-рой является простой алгеброй Ли над
к-рой является простой алгеброй Ли над  , а
, а  - такой инволютивный автоморфизм алгебры
- такой инволютивный автоморфизм алгебры  , что его неподвижные точки составляют максимальную компактно вложенную подалгебру; IV. (
, что его неподвижные точки составляют максимальную компактно вложенную подалгебру; IV. ( ), где
), где  - простая алгебра Ли над
- простая алгебра Ли над  , рассматриваемая как вещественная алгебра Ли, а
, рассматриваемая как вещественная алгебра Ли, а  - сопряжение алгебры gпо отношению к максимальной компактно вложенной подалгебре k, т. е. отображение
- сопряжение алгебры gпо отношению к максимальной компактно вложенной подалгебре k, т. е. отображение 
 Кроме того, если обозначить через
Кроме того, если обозначить через  алгебру, двойственную к (g,j), то (g,j) типа III и IV, если
алгебру, двойственную к (g,j), то (g,j) типа III и IV, если  типа I и II соответственно, и наоборот.
типа I и II соответственно, и наоборот. компактного типа, решается следующей теоремой.
компактного типа, решается следующей теоремой. - ортогональная симметрич. алгебра компактного типа, причем подалгебра k неподвижных точек автоморфизма
- ортогональная симметрич. алгебра компактного типа, причем подалгебра k неподвижных точек автоморфизма  не содержит идеалов алгебры g, отличных от
не содержит идеалов алгебры g, отличных от  . Пусть
. Пусть  - односвязная группа Ли с алгеброй Ли
- односвязная группа Ли с алгеброй Ли  - центр группы
- центр группы  - такой автоморфизм группы
- такой автоморфизм группы  , что
, что  и
и 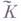 - множество всех неподвижных точек автоморфизма Ф. Для произвольной подгруппы Sгруппы
- множество всех неподвижных точек автоморфизма Ф. Для произвольной подгруппы Sгруппы  положим
положим 
 Г. с. р. п. М, связанные с
Г. с. р. п. М, связанные с  , совпадают с пространствами вида
, совпадают с пространствами вида  где
где 
 снабженными любой G-инвариантной метрикой. Здесь Sпробегает все подгруппы группы
снабженными любой G-инвариантной метрикой. Здесь Sпробегает все подгруппы группы  , а
, а  пробегает все такие подгруппы в
пробегает все такие подгруппы в  что
что 