"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЛОБАЛЬНАЯ СТРУКТУРА ТРАЕКТОРИЙ
Значение ГЛОБАЛЬНАЯ СТРУКТУРА ТРАЕКТОРИЙ в математической энциклопедии:
квадратичного дифференциала - описание поведения в целом траекторий положительного квадратичного дифференциала на конечной ориентированной римановой поверхности. Пусть R - конечная ориентированная риманова поверхность,  - положительный квадратичный дифференциал на R; пусть С- множество всех нулей и простых полюсов
- положительный квадратичный дифференциал на R; пусть С- множество всех нулей и простых полюсов  , а Н - множество всех полюсов
, а Н - множество всех полюсов  порядка
порядка  .
.
Траектории  образуют семейство F, обладающее многими свойствами регулярных семейств кривых. Это семейство кривых покрывает R, за исключением точек множества
образуют семейство F, обладающее многими свойствами регулярных семейств кривых. Это семейство кривых покрывает R, за исключением точек множества  , т. е. через каждую точку из
, т. е. через каждую точку из  проходит единственный элемент F. Поведение траекторий
проходит единственный элемент F. Поведение траекторий  в окрестности любой точки Rописывается локальной структурой траекторий квадратичного дифференциала. При рассмотрении глобальной структуры кривых семейства Fв точках
в окрестности любой точки Rописывается локальной структурой траекторий квадратичного дифференциала. При рассмотрении глобальной структуры кривых семейства Fв точках  существенную роль играют следующие объединения траекторий. Пусть Ф - объединение всех траекторий
существенную роль играют следующие объединения траекторий. Пусть Ф - объединение всех траекторий 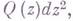 имеющих предельную концевую точку в нок-рой точке множества
имеющих предельную концевую точку в нок-рой точке множества  - подмножество Ф, являющееся объединением всех траекторий
- подмножество Ф, являющееся объединением всех траекторий  , к-рые имеют одну предельную концевую точку в точке множества Си вторую предельную концевую точку в точке множества
, к-рые имеют одну предельную концевую точку в точке множества Си вторую предельную концевую точку в точке множества  .
.
Множество Кна Rназ. F-множеством относительно  , если каждая траектория дифференциала
, если каждая траектория дифференциала  , пересекающаяся с К, полностью лежит в K. Внутреннее замыкание множества Копределяется как внутренность замыкания Ки обозначается К. Внутреннее замыкание F-множества снова является F-множеством. Концевой областью Еотносительно
, пересекающаяся с К, полностью лежит в K. Внутреннее замыкание множества Копределяется как внутренность замыкания Ки обозначается К. Внутреннее замыкание F-множества снова является F-множеством. Концевой областью Еотносительно  наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Ене содержит точек множества
наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Ене содержит точек множества  ; 2) Езаполнено траекториями дифференциала
; 2) Езаполнено траекториями дифференциала  , каждая из к-рых имеет предельную концевую точку в каждом из двух возможных направлений в данной точке
, каждая из к-рых имеет предельную концевую точку в каждом из двух возможных направлений в данной точке  Еконформно отображается функцией
Еконформно отображается функцией

на верхнюю или нижнюю полуплоскость плоскости  (в зависимости от выбора ветви корня). Из локальной структуры траекторий
(в зависимости от выбора ветви корня). Из локальной структуры траекторий  следует, что точка Адолжна быть полюсом дифференциала
следует, что точка Адолжна быть полюсом дифференциала  не ниже 3-го порядка.
не ниже 3-го порядка.
Полосообразной областью Sотносительно  наз. наибольшее связное открытое F- множество на Л, обладающее следующими свойствами: 1) 5 не содержит точек множества
наз. наибольшее связное открытое F- множество на Л, обладающее следующими свойствами: 1) 5 не содержит точек множества  ; 2) Sзаполнено траекториями дифференциала
; 2) Sзаполнено траекториями дифференциала  , каждая из к-рых имеет в одной точке
, каждая из к-рых имеет в одной точке  предельную концевую точку в одном направлении, а в другой (возможно, совпадающей с А).точке
предельную концевую точку в одном направлении, а в другой (возможно, совпадающей с А).точке  - предельную концевую точку в другом направлении; 3) Sконформно отображается функцией
- предельную концевую точку в другом направлении; 3) Sконформно отображается функцией

на полосу  где а, b- конечные действительные числа, а<b. Точки Аи Вмогут быть полюсами
где а, b- конечные действительные числа, а<b. Точки Аи Вмогут быть полюсами  порядка 2 и более.
порядка 2 и более.
Круговойобластью  относительно
относительно  наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1)
наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1)  содержит единственный двойной полюс Адифференциала
содержит единственный двойной полюс Адифференциала  ; 2)
; 2)  заполнено траекториями дифференциала
заполнено траекториями дифференциала  , каждая из к-рых является замкнутой жордановой кривой, отделяющей Аот границы
, каждая из к-рых является замкнутой жордановой кривой, отделяющей Аот границы  ; 3) при надлежащем выборе чисто мнимой постоянной сфункция
; 3) при надлежащем выборе чисто мнимой постоянной сфункция

дополненная значением нуль в точке А, отображает  конформно на круг
конформно на круг  , причем точка Апереходит в точку
, причем точка Апереходит в точку  .
.
Кольцевой областью D относительно  наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Dне содержит точек множества
наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Dне содержит точек множества  ; 2) Dзаполнено траекториями дифференциала
; 2) Dзаполнено траекториями дифференциала  , каждая из к-рых является замкнутой жордановой кривой; 3) при надлежащем выборе чисто мнимой постоянной сфункция
, каждая из к-рых является замкнутой жордановой кривой; 3) при надлежащем выборе чисто мнимой постоянной сфункция

отображает Dконформно на круговое кольцо 
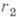

Плотностной областью  относительно
относительно  наз. наибольшее связное открытое
наз. наибольшее связное открытое  -множество на R, обладающее свойствами: 1)
-множество на R, обладающее свойствами: 1)  не содержит точек множества H; 2)
не содержит точек множества H; 2)  заполнено траекториями
заполнено траекториями  каждая из к-рых всюду плотна в
каждая из к-рых всюду плотна в  .
.
Справедлива основная структурная теорема (см. [2]). Пусть R - конечная ориентированная риманова поверхность,  - положительный квадратичный дифференциал на R, причем исключаются следующие возможные случаи и все конфигурации, получающиеся из них посредством конформного отображения:I. R есть z-сфера,
- положительный квадратичный дифференциал на R, причем исключаются следующие возможные случаи и все конфигурации, получающиеся из них посредством конформного отображения:I. R есть z-сфера,  П. Rесть z- сфера,
П. Rесть z- сфера,  К - положительное, а - действительное числа; III. Rесть тор, Q(z)dz2 регулярен на R. Тогда: 1)
К - положительное, а - действительное числа; III. Rесть тор, Q(z)dz2 регулярен на R. Тогда: 1)  состоит из конечного числа концевых, полосообразных, кольцевых, круговых и плотно-стных областей; 2) каждая такая область ограничена конечным числом траекторий вместе с точками, в к-рых последние встречаются; каждая граничная компонента такой области содержит точку множества С, за исключением граничных компонент круговой или кольцевой области, к-рые могут совпадать с граничными компонентами R; для полосообразной области два граничных элемента, выходящие из точек множества Н, разделяют границу на две части, на каждой из к-рых имеется точка множества С;3) каждый полюс
состоит из конечного числа концевых, полосообразных, кольцевых, круговых и плотно-стных областей; 2) каждая такая область ограничена конечным числом траекторий вместе с точками, в к-рых последние встречаются; каждая граничная компонента такой области содержит точку множества С, за исключением граничных компонент круговой или кольцевой области, к-рые могут совпадать с граничными компонентами R; для полосообразной области два граничных элемента, выходящие из точек множества Н, разделяют границу на две части, на каждой из к-рых имеется точка множества С;3) каждый полюс  порядка
порядка  имеет окрестность, покрываемую внутренним замыканием объединения m-2 концевых областей и конечного числа (возможно, равного нулю) полосообразных областей; 4) каждый полюс
имеет окрестность, покрываемую внутренним замыканием объединения m-2 концевых областей и конечного числа (возможно, равного нулю) полосообразных областей; 4) каждый полюс  порядка т=2 имеет окрестность, покрываемую внутренним замыканием объединения конечного числа полосообразных областей, или окрестность, содержащуюся в круговой области.
порядка т=2 имеет окрестность, покрываемую внутренним замыканием объединения конечного числа полосообразных областей, или окрестность, содержащуюся в круговой области.
Из этой теоремы непосредственно следует утверждение основной структурной теоремы Дж. Дженкинса (J. Jenkins) в первоначальной формулировке (см. [1]): в условиях сформулированной теоремы множество  состоит из конечного числа концевых, полосообразных, круговых и кольцевых областей. Большое внимание в ряде исследований теории однолистных функций уделяется доказательству того факта, что для рассматриваемого квадратичного дифференциала
состоит из конечного числа концевых, полосообразных, круговых и кольцевых областей. Большое внимание в ряде исследований теории однолистных функций уделяется доказательству того факта, что для рассматриваемого квадратичного дифференциала  множество
множество  пусто. Нахождение условий, обеспечивающих пустоту множества
пусто. Нахождение условий, обеспечивающих пустоту множества  , представляет и самостоятельный интерес. Пример квадратичного дифференциала
, представляет и самостоятельный интерес. Пример квадратичного дифференциала  на z-сфере, для к-рого множество
на z-сфере, для к-рого множество  пусто, дает следующая теорема о трех полюсах: если R есть z-сфера,
пусто, дает следующая теорема о трех полюсах: если R есть z-сфера,  - квадратичный дифференциал на Л, имеющий не более трех различных полюсов, то множество
- квадратичный дифференциал на Л, имеющий не более трех различных полюсов, то множество  пусто.
пусто.
Лит.:[1] Дженкинс Д ж., Однолистные функции и конформные отображения, пер. с англ., М., 1962; [2] Jеnkins J. A., "Illinois Math. J.", 1960, v. 4, № 3, p. 405-12.
Г. В. Кузьмина.

 - положительный квадратичный дифференциал на R; пусть С- множество всех нулей и простых полюсов
- положительный квадратичный дифференциал на R; пусть С- множество всех нулей и простых полюсов  , а Н - множество всех полюсов
, а Н - множество всех полюсов  порядка
порядка  .
. образуют семейство F, обладающее многими свойствами регулярных семейств кривых. Это семейство кривых покрывает R, за исключением точек множества
образуют семейство F, обладающее многими свойствами регулярных семейств кривых. Это семейство кривых покрывает R, за исключением точек множества  , т. е. через каждую точку из
, т. е. через каждую точку из  проходит единственный элемент F. Поведение траекторий
проходит единственный элемент F. Поведение траекторий  в окрестности любой точки Rописывается локальной структурой траекторий квадратичного дифференциала. При рассмотрении глобальной структуры кривых семейства Fв точках
в окрестности любой точки Rописывается локальной структурой траекторий квадратичного дифференциала. При рассмотрении глобальной структуры кривых семейства Fв точках  существенную роль играют следующие объединения траекторий. Пусть Ф - объединение всех траекторий
существенную роль играют следующие объединения траекторий. Пусть Ф - объединение всех траекторий 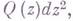 имеющих предельную концевую точку в нок-рой точке множества
имеющих предельную концевую точку в нок-рой точке множества  - подмножество Ф, являющееся объединением всех траекторий
- подмножество Ф, являющееся объединением всех траекторий  , к-рые имеют одну предельную концевую точку в точке множества Си вторую предельную концевую точку в точке множества
, к-рые имеют одну предельную концевую точку в точке множества Си вторую предельную концевую точку в точке множества  .
. , если каждая траектория дифференциала
, если каждая траектория дифференциала  , пересекающаяся с К, полностью лежит в K. Внутреннее замыкание множества Копределяется как внутренность замыкания Ки обозначается К. Внутреннее замыкание F-множества снова является F-множеством. Концевой областью Еотносительно
, пересекающаяся с К, полностью лежит в K. Внутреннее замыкание множества Копределяется как внутренность замыкания Ки обозначается К. Внутреннее замыкание F-множества снова является F-множеством. Концевой областью Еотносительно  наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Ене содержит точек множества
наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Ене содержит точек множества  ; 2) Езаполнено траекториями дифференциала
; 2) Езаполнено траекториями дифференциала  , каждая из к-рых имеет предельную концевую точку в каждом из двух возможных направлений в данной точке
, каждая из к-рых имеет предельную концевую точку в каждом из двух возможных направлений в данной точке  Еконформно отображается функцией
Еконформно отображается функцией 
 (в зависимости от выбора ветви корня). Из локальной структуры траекторий
(в зависимости от выбора ветви корня). Из локальной структуры траекторий  следует, что точка Адолжна быть полюсом дифференциала
следует, что точка Адолжна быть полюсом дифференциала  не ниже 3-го порядка.
не ниже 3-го порядка. наз. наибольшее связное открытое F- множество на Л, обладающее следующими свойствами: 1) 5 не содержит точек множества
наз. наибольшее связное открытое F- множество на Л, обладающее следующими свойствами: 1) 5 не содержит точек множества  ; 2) Sзаполнено траекториями дифференциала
; 2) Sзаполнено траекториями дифференциала  , каждая из к-рых имеет в одной точке
, каждая из к-рых имеет в одной точке  предельную концевую точку в одном направлении, а в другой (возможно, совпадающей с А).точке
предельную концевую точку в одном направлении, а в другой (возможно, совпадающей с А).точке  - предельную концевую точку в другом направлении; 3) Sконформно отображается функцией
- предельную концевую точку в другом направлении; 3) Sконформно отображается функцией
 где а, b- конечные действительные числа, а<b. Точки Аи Вмогут быть полюсами
где а, b- конечные действительные числа, а<b. Точки Аи Вмогут быть полюсами  порядка 2 и более.
порядка 2 и более. относительно
относительно  наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1)
наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1)  содержит единственный двойной полюс Адифференциала
содержит единственный двойной полюс Адифференциала  ; 2)
; 2)  заполнено траекториями дифференциала
заполнено траекториями дифференциала  , каждая из к-рых является замкнутой жордановой кривой, отделяющей Аот границы
, каждая из к-рых является замкнутой жордановой кривой, отделяющей Аот границы  ; 3) при надлежащем выборе чисто мнимой постоянной сфункция
; 3) при надлежащем выборе чисто мнимой постоянной сфункция 
 конформно на круг
конформно на круг  , причем точка Апереходит в точку
, причем точка Апереходит в точку  .
. наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Dне содержит точек множества
наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Dне содержит точек множества  ; 2) Dзаполнено траекториями дифференциала
; 2) Dзаполнено траекториями дифференциала  , каждая из к-рых является замкнутой жордановой кривой; 3) при надлежащем выборе чисто мнимой постоянной сфункция
, каждая из к-рых является замкнутой жордановой кривой; 3) при надлежащем выборе чисто мнимой постоянной сфункция 

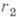

 относительно
относительно  наз. наибольшее связное открытое
наз. наибольшее связное открытое  -множество на R, обладающее свойствами: 1)
-множество на R, обладающее свойствами: 1)  не содержит точек множества H; 2)
не содержит точек множества H; 2)  заполнено траекториями
заполнено траекториями  каждая из к-рых всюду плотна в
каждая из к-рых всюду плотна в  .
. - положительный квадратичный дифференциал на R, причем исключаются следующие возможные случаи и все конфигурации, получающиеся из них посредством конформного отображения:I. R есть z-сфера,
- положительный квадратичный дифференциал на R, причем исключаются следующие возможные случаи и все конфигурации, получающиеся из них посредством конформного отображения:I. R есть z-сфера,  П. Rесть z- сфера,
П. Rесть z- сфера,  К - положительное, а - действительное числа; III. Rесть тор, Q(z)dz2 регулярен на R. Тогда: 1)
К - положительное, а - действительное числа; III. Rесть тор, Q(z)dz2 регулярен на R. Тогда: 1)  состоит из конечного числа концевых, полосообразных, кольцевых, круговых и плотно-стных областей; 2) каждая такая область ограничена конечным числом траекторий вместе с точками, в к-рых последние встречаются; каждая граничная компонента такой области содержит точку множества С, за исключением граничных компонент круговой или кольцевой области, к-рые могут совпадать с граничными компонентами R; для полосообразной области два граничных элемента, выходящие из точек множества Н, разделяют границу на две части, на каждой из к-рых имеется точка множества С;3) каждый полюс
состоит из конечного числа концевых, полосообразных, кольцевых, круговых и плотно-стных областей; 2) каждая такая область ограничена конечным числом траекторий вместе с точками, в к-рых последние встречаются; каждая граничная компонента такой области содержит точку множества С, за исключением граничных компонент круговой или кольцевой области, к-рые могут совпадать с граничными компонентами R; для полосообразной области два граничных элемента, выходящие из точек множества Н, разделяют границу на две части, на каждой из к-рых имеется точка множества С;3) каждый полюс  порядка
порядка  имеет окрестность, покрываемую внутренним замыканием объединения m-2 концевых областей и конечного числа (возможно, равного нулю) полосообразных областей; 4) каждый полюс
имеет окрестность, покрываемую внутренним замыканием объединения m-2 концевых областей и конечного числа (возможно, равного нулю) полосообразных областей; 4) каждый полюс  порядка т=2 имеет окрестность, покрываемую внутренним замыканием объединения конечного числа полосообразных областей, или окрестность, содержащуюся в круговой области.
порядка т=2 имеет окрестность, покрываемую внутренним замыканием объединения конечного числа полосообразных областей, или окрестность, содержащуюся в круговой области. состоит из конечного числа концевых, полосообразных, круговых и кольцевых областей. Большое внимание в ряде исследований теории однолистных функций уделяется доказательству того факта, что для рассматриваемого квадратичного дифференциала
состоит из конечного числа концевых, полосообразных, круговых и кольцевых областей. Большое внимание в ряде исследований теории однолистных функций уделяется доказательству того факта, что для рассматриваемого квадратичного дифференциала  множество
множество  пусто. Нахождение условий, обеспечивающих пустоту множества
пусто. Нахождение условий, обеспечивающих пустоту множества  , представляет и самостоятельный интерес. Пример квадратичного дифференциала
, представляет и самостоятельный интерес. Пример квадратичного дифференциала  на z-сфере, для к-рого множество
на z-сфере, для к-рого множество  пусто, дает следующая теорема о трех полюсах: если R есть z-сфера,
пусто, дает следующая теорема о трех полюсах: если R есть z-сфера,  - квадратичный дифференциал на Л, имеющий не более трех различных полюсов, то множество
- квадратичный дифференциал на Л, имеющий не более трех различных полюсов, то множество  пусто.
пусто.