|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЛАДКОСТИ МОДУЛЬЗначение ГЛАДКОСТИ МОДУЛЬ в математической энциклопедии: - модуль непрерывности производной порядка где где Нек-рые вопросы теории приближения функций могут получить окончательное решение только в терминах Г. м. порядка Модуль непрерывности таких функций удовлетворяет условию Лит.:[1] Бернштейн С. Н., Собр. сочинений, т. 1, с. 37, М., 1952; [2] Marchaud A., "J. math, pures et appl.", 1927, t. 6, p. 337-425; [3] Zygmund A., "Duke Math. J.", 1945, v. 12, p. 47-76; [4] Ефимов А. В., "Изв. АН СССР. Сер. матем.", 1957, т. 21, № 2, с. 283-88. А. В. Ефимов. |
|
|
|

 функции
функции  , определенной на банаховом пространстве X, т. е. выражение
, определенной на банаховом пространстве X, т. е. выражение 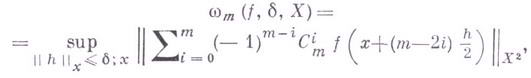
 . При т = 1 Г. и.- обычный непрерывности модуль функции f(x). Основные свойства Г. м. (для случая
. При т = 1 Г. и.- обычный непрерывности модуль функции f(x). Основные свойства Г. м. (для случая  - пространство непрерывных функций):
- пространство непрерывных функций):
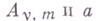 - постоянные, не зависящие от f.
- постоянные, не зависящие от f. . В теории приближения функций важен класс непрерывных периода 2p функций, Г. м. 2-го порядка к-рых удовлетворяет условию
. В теории приближения функций важен класс непрерывных периода 2p функций, Г. м. 2-го порядка к-рых удовлетворяет условию 

 , причем постоянная
, причем постоянная 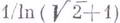 не может быть улучшена (см. [4]).
не может быть улучшена (см. [4]).