Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЛАВНОЕ ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕЗначение ГЛАВНОЕ ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕ в математической энциклопедии: фундаментальное решение удовлетворяющее условиям для нек-рых положительных постоянных а и Rпри Если коэффициенты Лит.:[1] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957. Ш. А. Алимов. |
|
|
|

 . определенного во всем пространстве
. определенного во всем пространстве  эллиптич. уравнения 2-го порядка
эллиптич. уравнения 2-го порядка 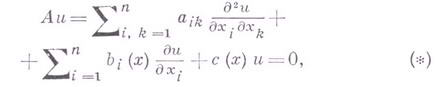

 .
. удовлетворяют в Е n условию Гёльдера и для
удовлетворяют в Е n условию Гёльдера и для  выполняется неравенство
выполняется неравенство  , то Г. ф. р. существует. В случае, когда коэффициенты оператора Аопределены в нек-рой ограниченной области с достаточно гладкой границей, их можно продолжить на все пространство Е n так, что у продолженного оператора Г. ф. р. будет существовать.
, то Г. ф. р. существует. В случае, когда коэффициенты оператора Аопределены в нек-рой ограниченной области с достаточно гладкой границей, их можно продолжить на все пространство Е n так, что у продолженного оператора Г. ф. р. будет существовать.