"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИПЕРГРАФ
Значение ГИПЕРГРАФ в математической энциклопедии:
- обобщение понятия графа. Г. задается множеством V, элементы к-рого наз. вершинами, и семейством  подмножеств множества V, называемых ребрами Г.; Г. обозначается
подмножеств множества V, называемых ребрами Г.; Г. обозначается  Понятие Г. является вариантом давно известных понятий комплекса, блок-схемы, а также понятия сети.
Понятие Г. является вариантом давно известных понятий комплекса, блок-схемы, а также понятия сети.
Две вершины  и
и  Г. наз. смежными, если существует ребро, содержащее эти вершины. Вершина
Г. наз. смежными, если существует ребро, содержащее эти вершины. Вершина  и ребро Е Т. наз. инцидентными, если
и ребро Е Т. наз. инцидентными, если  Г. Нс пвершинами и требрами можно задать матрицей инцидентности, т. е. матрицей
Г. Нс пвершинами и требрами можно задать матрицей инцидентности, т. е. матрицей 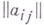 размера
размера  , в к-рой столбцы соответствуют ребрам, а строки - вершинам Г. и
, в к-рой столбцы соответствуют ребрам, а строки - вершинам Г. и

Всякой прямоугольной матрице Миз нулей и единиц можно сопоставить Г., для к-рого Мявляется матрицей инцидентности. Г.  наз. двойственным по отношению к Г. Н, если матрица инцидентности Г.
наз. двойственным по отношению к Г. Н, если матрица инцидентности Г.  получается транспонированием матрицы инцидентности Г. Н. Число ребер Г., инцидентных данной вершине, наз. степенью вершины.
получается транспонированием матрицы инцидентности Г. Н. Число ребер Г., инцидентных данной вершине, наз. степенью вершины.

Степенью ребра наз. число вершин Г., инцидентных этому ребру. Г.  наз.
наз.
подгиперграфом Г.  , если
, если  и вершина
и вершина  из
из  и ребро
и ребро  из
из  инцидентны в Г.
инцидентны в Г. тогда и только тогда, когда они инцидентны в Г.
тогда и только тогда, когда они инцидентны в Г. Г. можно изобразить на плоскости, сопоставляя вершинам Г. точки плоскости, а ребрам - связные области, охватывающие вершины, инцидентные этим ребрам. Напр., Г. H с множеством вершин
Г. можно изобразить на плоскости, сопоставляя вершинам Г. точки плоскости, а ребрам - связные области, охватывающие вершины, инцидентные этим ребрам. Напр., Г. H с множеством вершин  и семейством ребер
и семейством ребер

можно изобразить на плоскости, как показано на рис. Г. Нможно представлять графом двудольным К (Н), в к-ром вершины одной доли  соответствуют вершинам Г., а вершины другой доли
соответствуют вершинам Г., а вершины другой доли 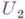 - ребрам Г. Н. При этом две вершины
- ребрам Г. Н. При этом две вершины  из
из  и
и  из
из  соединены в графе К(Н).ребром, если вершина Г., соответствующая вершине
соединены в графе К(Н).ребром, если вершина Г., соответствующая вершине  , инцидентна ребру Г., соответствующему вершине
, инцидентна ребру Г., соответствующему вершине 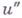 . Г. является графом, если каждое ребро его имеет степень, равную 2. Важным частным случаем понятия "Г." является матроид.
. Г. является графом, если каждое ребро его имеет степень, равную 2. Важным частным случаем понятия "Г." является матроид.
Многие понятия теории графов, такие, как связность, планарность, хроматин, число, числа внутренней и внешней устойчивости, переносятся и на Г. На Г. переносятся также многие утверждения, справедливые для графов.
Лит.:[1] Зыков А. А., "Успехи матем. наук", 1974, т. 29, в. 6, с. 89-154; [2] Веrge С., Graphes et hypergraphes, р 1970 А. А. Сапоженко.

 подмножеств множества V, называемых ребрами Г.; Г. обозначается
подмножеств множества V, называемых ребрами Г.; Г. обозначается  Понятие Г. является вариантом давно известных понятий комплекса, блок-схемы, а также понятия сети.
Понятие Г. является вариантом давно известных понятий комплекса, блок-схемы, а также понятия сети. и
и  Г. наз. смежными, если существует ребро, содержащее эти вершины. Вершина
Г. наз. смежными, если существует ребро, содержащее эти вершины. Вершина  и ребро Е Т. наз. инцидентными, если
и ребро Е Т. наз. инцидентными, если  Г. Нс пвершинами и требрами можно задать матрицей инцидентности, т. е. матрицей
Г. Нс пвершинами и требрами можно задать матрицей инцидентности, т. е. матрицей 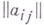 размера
размера  , в к-рой столбцы соответствуют ребрам, а строки - вершинам Г. и
, в к-рой столбцы соответствуют ребрам, а строки - вершинам Г. и 
 наз. двойственным по отношению к Г. Н, если матрица инцидентности Г.
наз. двойственным по отношению к Г. Н, если матрица инцидентности Г.  получается транспонированием матрицы инцидентности Г. Н. Число ребер Г., инцидентных данной вершине, наз. степенью вершины.
получается транспонированием матрицы инцидентности Г. Н. Число ребер Г., инцидентных данной вершине, наз. степенью вершины. 
 наз.
наз.  , если
, если  и вершина
и вершина  из
из  и ребро
и ребро  из
из  инцидентны в Г.
инцидентны в Г. тогда и только тогда, когда они инцидентны в Г.
тогда и только тогда, когда они инцидентны в Г. Г. можно изобразить на плоскости, сопоставляя вершинам Г. точки плоскости, а ребрам - связные области, охватывающие вершины, инцидентные этим ребрам. Напр., Г. H с множеством вершин
Г. можно изобразить на плоскости, сопоставляя вершинам Г. точки плоскости, а ребрам - связные области, охватывающие вершины, инцидентные этим ребрам. Напр., Г. H с множеством вершин  и семейством ребер
и семейством ребер 
 соответствуют вершинам Г., а вершины другой доли
соответствуют вершинам Г., а вершины другой доли 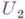 - ребрам Г. Н. При этом две вершины
- ребрам Г. Н. При этом две вершины  из
из  и
и  из
из  соединены в графе К(Н).ребром, если вершина Г., соответствующая вершине
соединены в графе К(Н).ребром, если вершина Г., соответствующая вершине  , инцидентна ребру Г., соответствующему вершине
, инцидентна ребру Г., соответствующему вершине 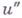 . Г. является графом, если каждое ребро его имеет степень, равную 2. Важным частным случаем понятия "Г." является матроид.
. Г. является графом, если каждое ребро его имеет степень, равную 2. Важным частным случаем понятия "Г." является матроид.