Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИПЕРГЕОМЕТРИЧЕСКИЙ РЯДЗначение ГИПЕРГЕОМЕТРИЧЕСКИЙ РЯД в математической энциклопедии: , ряд Гаусса,- ряд вида
Г. р. имеет смысл, если g не равно нулю или целому отрицательному числу; он сходится при где Г (z) - гамма-функция. Аналитич. функция, определяемая с помощью Г. р., наз. гипергеометрической функцией. Обобщенным гипергеометрическим рядом наз. ряд вида где |
|
|
|

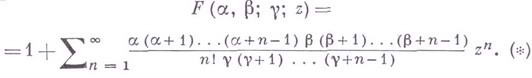
 . Если, кроме того,
. Если, кроме того,  то Г. р. сходится и при z= 1. В этом случае справедлива формула Гаусса
то Г. р. сходится и при z= 1. В этом случае справедлива формула Гаусса 

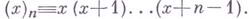 В этих обозначениях ряд (*) записывается как
В этих обозначениях ряд (*) записывается как  Э. А. Чистова.
Э. А. Чистова.