|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИПЕРБОЛИЧЕСКОЙ МЕТРИКИ ПРИНЦИПЗначение ГИПЕРБОЛИЧЕСКОЙ МЕТРИКИ ПРИНЦИП в математической энциклопедии: пусть области Dи Gлежат соответственно в плоскостях Равенство в какой-либо точке В формулировке Г. м. п. предположение регулярности функции f(z) в Dможет быть заменено более общим предположением: f(z) - аналитич. функция, определенная в Dкаким-либо своим элементом и продол-жимая в D по любому пути. Этот же принцип можно сформулировать также относительно поведения гиперболич. длины кривых, гиперболич. расстояния или гиперболич. площади при указанном отображении. Именно, если L- спрямляемая кривая в D, то (в обозначениях статьи Гиперболическая метрика)
Если В каждом из этих неравенств равенство достигается только в указанном выше случае. Приведенный выше результат относительно гиперболич. расстояния показывает, что при отображении Этот результат распространяет на случай многосвязных областей следующий факт теории конформного отображения (инвариантная форма леммы Шварца): при отображении круга Г. м. п. следующим образом связан с Линделёфа принципом. Если области Dи G обладают функциями Грина и односвязны, то оба принципа совпадают. Если же Dодносвязна, a Gмногосвязна, то Г. м. п. дает более точную оценку области, в к-рой содержится образ гиперболич. круга в D, определяемого неравенством |
|
|
|

 и
и  и имеют каждая не менее чем по три граничные точки, пусть
и имеют каждая не менее чем по три граничные точки, пусть  - функция, регулярная в Dи принимающая значения в G, и пусть
- функция, регулярная в Dи принимающая значения в G, и пусть  и
и  - линейные элементы в гиперболич. метрике областей D и G в точках соответственно
- линейные элементы в гиперболич. метрике областей D и G в точках соответственно  и
и  ; тогда справедливо неравенство
; тогда справедливо неравенство 
 имеет место только в том случае, если
имеет место только в том случае, если  в D, где функция
в D, где функция 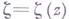 конформно отображает область Dна круг
конформно отображает область Dна круг  , а функция
, а функция  конформно отображает круг Ена область G. Г. м. п. обобщает Шварца лемму на многосвязные области, в к-рых может быть определена гиперболич. метрика.
конформно отображает круг Ена область G. Г. м. п. обобщает Шварца лемму на многосвязные области, в к-рых может быть определена гиперболич. метрика.
 и
и  - две точки области D, то Если В - область
- две точки области D, то Если В - область  в D, то
в D, то 
 образ гиперболич. круга с центром в точке
образ гиперболич. круга с центром в точке 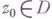 содержится в гиперболич. круге с центром в точке
содержится в гиперболич. круге с центром в точке  того же гиперболпч. радиуса.
того же гиперболпч. радиуса. регулярной в нем
регулярной в нем 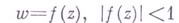 функцией в
функцией в  , гиперболич. расстояние между образами точек
, гиперболич. расстояние между образами точек  и
и  круга Ене превосходит гиперболич. расстояния между самими точками
круга Ене превосходит гиперболич. расстояния между самими точками  и
и  и равно этому расстоянию только в случае дробно-линейного преобразования круга Ена себя.
и равно этому расстоянию только в случае дробно-линейного преобразования круга Ена себя. при отображении
при отображении  (где через
(где через  обозначена функция Грина области Dс лога-рифмич. полюсом в точке
обозначена функция Грина области Dс лога-рифмич. полюсом в точке  ). Кроме того, Г. м. п. применим и тогда, когда нельзя говорить о принципе Линделёфа, напр., в случае области, обладающей по крайней мере тремя граничными точками, но не имеющей функции Грина. Г. В. Кузьмина.
). Кроме того, Г. м. п. применим и тогда, когда нельзя говорить о принципе Линделёфа, напр., в случае области, обладающей по крайней мере тремя граничными точками, но не имеющей функции Грина. Г. В. Кузьмина.