" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД

Значение ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД в математической энциклопедии:

незамкнутая нецентральная поверхность второго порядка. В надлежащей системе координат (см. рис.) уравнение Г. п. имеет вид:

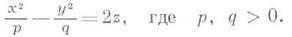
Сечения Г. п. плоскостями, параллельными плоскостям 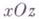и , являются параболами, а сечения плоскостями, параллельными плоскости ,- гиперболами (плоскостью 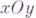- двумя прямыми). Ось симметрии Т. п. наз. его осью; точка пересечения Г. п. с осью наз. вершиной Г. п. Если p = q, то Г. п. имеет две оси симметрии. Г. п.- линейчатая поверхность;

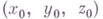уравнения прямолинейных образующих, проходящих через данную точку Г. п., имеют вид:

А. Б. Иванов.