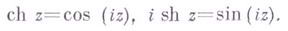|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИЗначение ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ в математической энциклопедии: функции, определяемые формулами: Иногда рассматривается также гиперболический тангенс; Другие обозначения: sinh x,Sh x,cosh x, Ch x,tgh x,tanh x,Th x. Графики см. на рис. 1. Основные соотношения:
Геометрическая интерпретация Г. ф. аналогична интерпретации тригонометрических функций (рис. 2). Параметрич. уравнения Производные и основные интегралы от Г. ф.:
Во всей плоскости комплексного переменного z Г. ф. таким образом, Имеются обширные таблицы для Г. ф. Значения Г. ф. можно получить также из таблиц для е х и е -х. Лит.:[1] Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, 2 изд., пер. с нем., М., 1968; [2] Таблицы круговых и гиперболических синусов и косинусов в радиацией мере угла, М., 1958; [3] Таблицы е x и е -x, М., 1955. В. И. Битюцков. |
|
|
|

 - гиперболический синус,
- гиперболический синус, -г иперболический косинус.
-г иперболический косинус.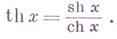

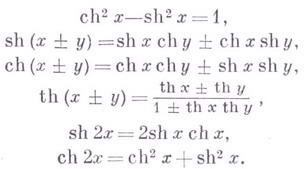
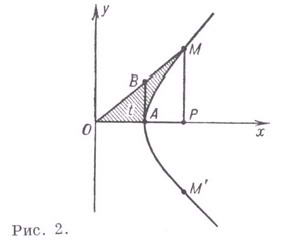
 гиперболы позволяют истолковать абсциссу
гиперболы позволяют истолковать абсциссу  и ординату
и ординату  точки Мравносторонней гиперболы
точки Мравносторонней гиперболы  как гиперболнч. косинус и синус; гиперболич. тангенс-отрезок АВ. Параметр tравен удвоенной площади сектора ОАМ, где AM - дуга гиперболы. Для точки
как гиперболнч. косинус и синус; гиперболич. тангенс-отрезок АВ. Параметр tравен удвоенной площади сектора ОАМ, где AM - дуга гиперболы. Для точки  (при
(при  ) параметр tотрицателен. Обратные гиперболические функции определяются формулами:
) параметр tотрицателен. Обратные гиперболические функции определяются формулами: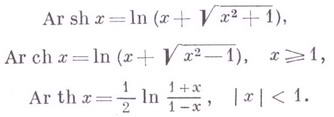
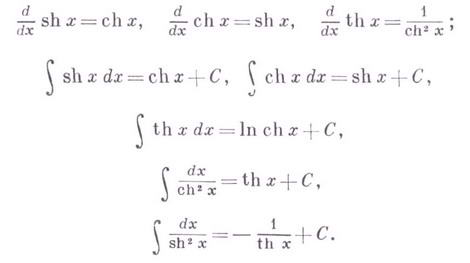
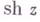 и
и 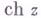 могут быть определены рядами:
могут быть определены рядами: