"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИПЕРБОЛИЧЕСКАЯ ТОЧКА
Значение ГИПЕРБОЛИЧЕСКАЯ ТОЧКА в математической энциклопедии:
- 1) Г. т. поверхности- точка, в к-рой соприкасающийся параболоид является гиперболич. параболоидом. В Г. т. индикатриса кривизны представляет собой пару сопряженных гипербол. Е. <В. Шикин.
2).Г. т. динамической системы - такая точка  , принадлежащая области определения системы вида
, принадлежащая области определения системы вида 
что  , а матрица А, равная значению
, а матрица А, равная значению  в точке
в точке  , имеет kсобственных значений с положительной: действительной частью и
, имеет kсобственных значений с положительной: действительной частью и  собственных значений с отрицательной действительной частью,
собственных значений с отрицательной действительной частью,  В окрестности Г. т. существует
В окрестности Г. т. существует  -мерная инвариантная поверхность
-мерная инвариантная поверхность  , образованная решениями системы (*), к-рые при
, образованная решениями системы (*), к-рые при 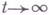 асимптотически приближаются к точке
асимптотически приближаются к точке  , и k-мерная инвариантная поверхность
, и k-мерная инвариантная поверхность  , образованная решениями системы (*), к-рые асимптотически приближаются к точке
, образованная решениями системы (*), к-рые асимптотически приближаются к точке  при
при  Поведение траекторий системы (*) в достаточно малой окрестности Г. т. характеризуется следующей теоремой [4]: существует гомеоморфизм нек-рой окрестности Г. т. в нек-рую окрестность точки
Поведение траекторий системы (*) в достаточно малой окрестности Г. т. характеризуется следующей теоремой [4]: существует гомеоморфизм нек-рой окрестности Г. т. в нек-рую окрестность точки 
 , переводящий траектории системы (*) в траектории линейной системы
, переводящий траектории системы (*) в траектории линейной системы  Г. т. для диффеоморфизма, обладающего неподвижной точкой, определяется требованием отсутствия равных по модулю единице собственных значений у линейной части диффеоморфизма в рассматриваемой неподвижной точке. Таким образом, Г. т. системы (*) остаются Г. т. диффеоморфизма, порождаемого сдвигом, вдоль траекторий системы (*).
Г. т. для диффеоморфизма, обладающего неподвижной точкой, определяется требованием отсутствия равных по модулю единице собственных значений у линейной части диффеоморфизма в рассматриваемой неподвижной точке. Таким образом, Г. т. системы (*) остаются Г. т. диффеоморфизма, порождаемого сдвигом, вдоль траекторий системы (*).
Лит.:[1] Пуанкаре А., О кривых, определяемых дифференциальными уравнениями, пер. с франц., М.-Л., 1947; [2] Ляпунов А. М., Общая задача об устойчивости движения, М.-Л., 1950; [3] Коддингтон Э. А., Левинсон Н., Теория обыкновенных дифференциальных уравнений, пер. с англ., М., 1958; [4] X артман Ф., Обыкновенные-дифференциальные уравнения, пер. с англ., М., 1970.
В. К. Мельников.

 , принадлежащая области определения системы вида
, принадлежащая области определения системы вида 
 , а матрица А, равная значению
, а матрица А, равная значению  в точке
в точке  , имеет kсобственных значений с положительной: действительной частью и
, имеет kсобственных значений с положительной: действительной частью и  собственных значений с отрицательной действительной частью,
собственных значений с отрицательной действительной частью,  В окрестности Г. т. существует
В окрестности Г. т. существует  -мерная инвариантная поверхность
-мерная инвариантная поверхность  , образованная решениями системы (*), к-рые при
, образованная решениями системы (*), к-рые при 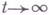 асимптотически приближаются к точке
асимптотически приближаются к точке  , и k-мерная инвариантная поверхность
, и k-мерная инвариантная поверхность  , образованная решениями системы (*), к-рые асимптотически приближаются к точке
, образованная решениями системы (*), к-рые асимптотически приближаются к точке  при
при  Поведение траекторий системы (*) в достаточно малой окрестности Г. т. характеризуется следующей теоремой [4]: существует гомеоморфизм нек-рой окрестности Г. т. в нек-рую окрестность точки
Поведение траекторий системы (*) в достаточно малой окрестности Г. т. характеризуется следующей теоремой [4]: существует гомеоморфизм нек-рой окрестности Г. т. в нек-рую окрестность точки 
 , переводящий траектории системы (*) в траектории линейной системы
, переводящий траектории системы (*) в траектории линейной системы  Г. т. для диффеоморфизма, обладающего неподвижной точкой, определяется требованием отсутствия равных по модулю единице собственных значений у линейной части диффеоморфизма в рассматриваемой неподвижной точке. Таким образом, Г. т. системы (*) остаются Г. т. диффеоморфизма, порождаемого сдвигом, вдоль траекторий системы (*).
Г. т. для диффеоморфизма, обладающего неподвижной точкой, определяется требованием отсутствия равных по модулю единице собственных значений у линейной части диффеоморфизма в рассматриваемой неподвижной точке. Таким образом, Г. т. системы (*) остаются Г. т. диффеоморфизма, порождаемого сдвигом, вдоль траекторий системы (*).