|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИЛЬБЕРТА - ШМИДТА ОПЕРАТОРЗначение ГИЛЬБЕРТА - ШМИДТА ОПЕРАТОР в математической энциклопедии: оператор А, действующий в гильбертовом пространстве H такой, что для любого ортонормированного базиса (достаточно, однако, справедливости этого для нек-рого базиса). Г.- Ш. о. является компактным оператором, для s-чисел к-рого при этом Если
- его регуляризованный характеристический определитель, то выполнено неравенство Карлемана Типичный представитель Г.- Ш. о.- Гильберта - Шмидта интегральный оператор (откуда и название). М. И. Войцеховский. |
|
|
|

 в Нвыполнено условие:
в Нвыполнено условие: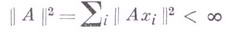
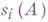 и для собственных чисел
и для собственных чисел 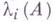 имеет место:
имеет место: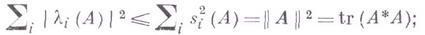
 оказывается ядерным оператором (здесь
оказывается ядерным оператором (здесь 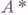 - оператор, сопряженный к 4, а
- оператор, сопряженный к 4, а 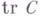 - след оператора С). Совокупность всех Г.- Ш. о. пространства Аобразует гильбертово пространство со скалярным произведением
- след оператора С). Совокупность всех Г.- Ш. о. пространства Аобразует гильбертово пространство со скалярным произведением 
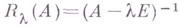 - резольвента А, а
- резольвента А, а 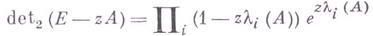
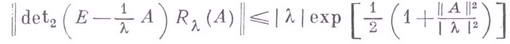 .
.