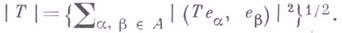" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ГИЛЬБЕРТА - ШМИДТА НОРМА

Значение ГИЛЬБЕРТА - ШМИДТА НОРМА в математической энциклопедии:

норма линейного оператора Т, действующего из гильбертова пространства Нв гильбертово пространство , имеющая вид , где - ортонор-мированный базис в H. Г.- Ш. н. удовлетворяет всем аксиомам нормы и не зависит от выбора базиса; ее свойства: - норма оператора Тв гильбертовом пространстве; если то

Лит.:[1] Данфорд Н., Шварц Д ж., Линейные операторы, ч. 2, пер. с англ., М., 1966; [2] Гельфанд И. М., Виленкин Н. Я., Некоторые применения гармонического анализа. Оснащенные гильбертовы пространства, М., 1961.

В. Б. Коротков.