"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИЛЬБЕРТА - ШМИДТА ИНТЕГРАЛЬНЫЙ ОПЕРАТОР
Значение ГИЛЬБЕРТА - ШМИДТА ИНТЕГРАЛЬНЫЙ ОПЕРАТОР в математической энциклопедии:
- ограниченный линейный интегральный оператор Т, действующий из пространства  в
в  и представимый в виде
и представимый в виде

где  - ядро оператора (см. [1]).
- ядро оператора (см. [1]).
Впервые такого рода операторы рассматривались Д. Гильбертом (D. Hilbert) и Э. Шмидтом (Е. Schmidt) в 1907. Г.- Ш. и. о. является вполне непрерывным оператором (см. [2]). Сопряженный к нему оператор также есть Г.- Ш. и. о. с ядром  [3]. Г.- Ш. и. о. будет самвсопряженным оператором тогда и только тогда, когда
[3]. Г.- Ш. и. о. будет самвсопряженным оператором тогда и только тогда, когда  для почти всех
для почти всех  (относительно
(относительно  ). Для самосопряженного Г.- Ш. и. о. и его ядра имеют место разложения
). Для самосопряженного Г.- Ш. и. о. и его ядра имеют место разложения

где  - ортонормированная система собственных функций оператора Т, отвечающих собственным значениям
- ортонормированная система собственных функций оператора Т, отвечающих собственным значениям  ряд (1) сходится по норме
ряд (1) сходится по норме  а ряд (2) сходится по норме
а ряд (2) сходится по норме  (см. [4]). В условиях Мерсера теоремы ряд (2) сходится абсолютно и равномерно (см. [5]).
(см. [4]). В условиях Мерсера теоремы ряд (2) сходится абсолютно и равномерно (см. [5]).
Если

то ряд (1) сходится абсолютно и равномерно (см. [4]). Линейный оператор
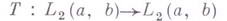
является Г.- Ш. и. о. тогда и только тогда, когда  есть
есть  -линейный оператор (см. [6]). Если
-линейный оператор (см. [6]). Если  есть
есть  -конечная мера, то линейный оператор
-конечная мера, то линейный оператор
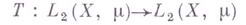
является Г.- Ш. и. о. тогда и только тогда, когда существует такая функция . что для всех
что для всех  неравенство
неравенство

справедливо для почти всех  (относительно меры
(относительно меры  ) [7]. Таким образом, Г.- Ш. и. о. образуют двусторонний идеал в банаховой алгебре всех линейных ограниченных операторов, действующих из
) [7]. Таким образом, Г.- Ш. и. о. образуют двусторонний идеал в банаховой алгебре всех линейных ограниченных операторов, действующих из  в Г.-
в Г.-  Ш. и. о. играют важную роль в теории интегральных уравнений и в теории краевых задач (см. [8], [9]), так как операторы, возникающие во многих задачах математич. физики, либо сами являются Г.- Ш. и. о., либо их итерации нек-рого порядка обладают этим свойством. Естественным обобщением Г.- Ш. и. о. является Гильберта - Шмидта оператор. Лит.:[1] Данфорд Н., Шварц Д ж. , Линейные операторы, ч. 2, пер. с англ., М.,.1966; [2] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [3] Stоnе М. Н., Linear Transformations in Hilbert Space and their Applications to Analysis, N. Y., 1964; [4] Рисе Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; [5] Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964; [6] Канторович Л. В. [и др.].. Функциональный анализ в полуупорядоченных пространствах, М.- Л., 1950; [7] Wеidmann J., Manuscripta Math., 1970, v. 2, № 1, p. 1-38; [8] Морен К., Методы гильбертова пространства, пер. с польск., М., 1965; [9] Березанский Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965. В. Б. Коротков.
Ш. и. о. играют важную роль в теории интегральных уравнений и в теории краевых задач (см. [8], [9]), так как операторы, возникающие во многих задачах математич. физики, либо сами являются Г.- Ш. и. о., либо их итерации нек-рого порядка обладают этим свойством. Естественным обобщением Г.- Ш. и. о. является Гильберта - Шмидта оператор. Лит.:[1] Данфорд Н., Шварц Д ж. , Линейные операторы, ч. 2, пер. с англ., М.,.1966; [2] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [3] Stоnе М. Н., Linear Transformations in Hilbert Space and their Applications to Analysis, N. Y., 1964; [4] Рисе Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; [5] Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964; [6] Канторович Л. В. [и др.].. Функциональный анализ в полуупорядоченных пространствах, М.- Л., 1950; [7] Wеidmann J., Manuscripta Math., 1970, v. 2, № 1, p. 1-38; [8] Морен К., Методы гильбертова пространства, пер. с польск., М., 1965; [9] Березанский Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965. В. Б. Коротков.

 в
в  и представимый в виде
и представимый в виде 
 - ядро оператора (см. [1]).
- ядро оператора (см. [1]). [3]. Г.- Ш. и. о. будет самвсопряженным оператором тогда и только тогда, когда
[3]. Г.- Ш. и. о. будет самвсопряженным оператором тогда и только тогда, когда  для почти всех
для почти всех  (относительно
(относительно  ). Для самосопряженного Г.- Ш. и. о. и его ядра имеют место разложения
). Для самосопряженного Г.- Ш. и. о. и его ядра имеют место разложения 
 - ортонормированная система собственных функций оператора Т, отвечающих собственным значениям
- ортонормированная система собственных функций оператора Т, отвечающих собственным значениям  ряд (1) сходится по норме
ряд (1) сходится по норме  а ряд (2) сходится по норме
а ряд (2) сходится по норме  (см. [4]). В условиях Мерсера теоремы ряд (2) сходится абсолютно и равномерно (см. [5]).
(см. [4]). В условиях Мерсера теоремы ряд (2) сходится абсолютно и равномерно (см. [5]).
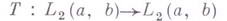
 есть
есть  -линейный оператор (см. [6]). Если
-линейный оператор (см. [6]). Если  есть
есть  -конечная мера, то линейный оператор
-конечная мера, то линейный оператор 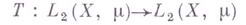
 что для всех
что для всех  неравенство
неравенство 
 (относительно меры
(относительно меры  ) [7]. Таким образом, Г.- Ш. и. о. образуют двусторонний идеал в банаховой алгебре всех линейных ограниченных операторов, действующих из
) [7]. Таким образом, Г.- Ш. и. о. образуют двусторонний идеал в банаховой алгебре всех линейных ограниченных операторов, действующих из  в Г.-
в Г.-  Ш. и. о. играют важную роль в теории интегральных уравнений и в теории краевых задач (см. [8], [9]), так как операторы, возникающие во многих задачах математич. физики, либо сами являются Г.- Ш. и. о., либо их итерации нек-рого порядка обладают этим свойством. Естественным обобщением Г.- Ш. и. о. является Гильберта - Шмидта оператор. Лит.:[1] Данфорд Н., Шварц Д ж. , Линейные операторы, ч. 2, пер. с англ., М.,.1966; [2] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [3] Stоnе М. Н., Linear Transformations in Hilbert Space and their Applications to Analysis, N. Y., 1964; [4] Рисе Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; [5] Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964; [6] Канторович Л. В. [и др.].. Функциональный анализ в полуупорядоченных пространствах, М.- Л., 1950; [7] Wеidmann J., Manuscripta Math., 1970, v. 2, № 1, p. 1-38; [8] Морен К., Методы гильбертова пространства, пер. с польск., М., 1965; [9] Березанский Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965. В. Б. Коротков.
Ш. и. о. играют важную роль в теории интегральных уравнений и в теории краевых задач (см. [8], [9]), так как операторы, возникающие во многих задачах математич. физики, либо сами являются Г.- Ш. и. о., либо их итерации нек-рого порядка обладают этим свойством. Естественным обобщением Г.- Ш. и. о. является Гильберта - Шмидта оператор. Лит.:[1] Данфорд Н., Шварц Д ж. , Линейные операторы, ч. 2, пер. с англ., М.,.1966; [2] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [3] Stоnе М. Н., Linear Transformations in Hilbert Space and their Applications to Analysis, N. Y., 1964; [4] Рисе Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; [5] Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964; [6] Канторович Л. В. [и др.].. Функциональный анализ в полуупорядоченных пространствах, М.- Л., 1950; [7] Wеidmann J., Manuscripta Math., 1970, v. 2, № 1, p. 1-38; [8] Морен К., Методы гильбертова пространства, пер. с польск., М., 1965; [9] Березанский Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965. В. Б. Коротков.