|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИЛЬБЕРТА ТЕОВИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙЗначение ГИЛЬБЕРТА ТЕОВИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ в математической энциклопедии: - общая теория линейных интегральных уравнений II рода построенная Д. Гильбертом [1] на базе созданной им теории линейных и билинейных форм с бесконечным числом переменных. Основная идея Г. т. и. у. состоит в следующем. Пусть имеется полная ортонормированная система функций
Решение интегрального уравнения (1) эквивалентно решению бесконечной системы линейных алгебраич. уравнений: При этом имеются в виду только те решения этой системы, для к-рых
т. е. система рассматривается в гильбертовом пространстве. Исследование системы (2) в гильбертовом пространстве позволяет изучить свойства уравнения (1). В Г. т. и. у. были обоснованы экстремальные свойства собственных значений интегральных уравнений с эрмитовыми ядрами. Лит.:[l] Hilbert D., Grundzuge einer allgemeinen Theorie der linearen Integralgleichungen, 2 Aufl., Lpz.- В., 1924. Б. В. Хведелидзе. |
|
|
|


 на интервале
на интервале 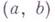 и пусть
и пусть

