|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИЛЬБЕРТА СХЕМАЗначение ГИЛЬБЕРТА СХЕМА в математической энциклопедии: - конструкция в алгебраич. геометрии, позволяющая снабжать множество замкнутых подмногообразий проективного пространства с заданным Гильберта многочленом структурой алгебраич. многообразия. Более точно, пусть X - проективная схема над локально нётеровой схемой Для любого полинома Лит.:[1] Мамфорд Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [2] Дьёдонне Ж., Керрол Дж., Мамфорд Д., Геометрическая теория инвариантов, пер. с англ., М., 1974; [3] Grоthendieck A., "Seminaire Bourbaki", aim. 13, N. Y.-Amst., 1966, p. 1-28; [4] Hartshorne R., "Publ. math. IHES", 1966, t. 29, p. 261-304; [5] Итоги науки. Алгебра. Геометрия. Топология, т. 10, 1972, с. 47-113. И. В. Долгачев. |
|
|
|

 и
и  - функтор, сопоставляющий каждой S-схеме S' множество замкнутых подсхем схемы
- функтор, сопоставляющий каждой S-схеме S' множество замкнутых подсхем схемы  плоских над
плоских над  . Функтор
. Функтор  представим локально нётеровой схемой, к-рая наз. схемой Гильберта S-схемы Xи обозначается через
представим локально нётеровой схемой, к-рая наз. схемой Гильберта S-схемы Xи обозначается через  (см. [4]). По определению представимых функторов в алгебраич. геометрии, для любой
(см. [4]). По определению представимых функторов в алгебраич. геометрии, для любой  -схемы
-схемы  имеет место биекция
имеет место биекция 
 . В частности, если S - спектр поля k,a
. В частности, если S - спектр поля k,a  - проективное пространство над k. то множество рациональных k-точек схемы
- проективное пространство над k. то множество рациональных k-точек схемы  находится во взаимно однозначном соответствии с множеством замкнутых подмногообразий в
находится во взаимно однозначном соответствии с множеством замкнутых подмногообразий в  .
. с рациональными коэффициентами функтор
с рациональными коэффициентами функтор  содержит подфунк-тор
содержит подфунк-тор  , выделяющий в множестве
, выделяющий в множестве  подмножество подсхем
подмножество подсхем  таких, что для любой точки
таких, что для любой точки  слой
слой  проекций
проекций  на
на  имеет
имеет 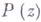 в качестве своего многочлена Гильберта. Функтор
в качестве своего многочлена Гильберта. Функтор  представим схемой
представим схемой  , проективной над S. Схема
, проективной над S. Схема  является прямой суммой схем
является прямой суммой схем  по всем
по всем  . Для любой связной базисной схемы Sсхема
. Для любой связной базисной схемы Sсхема  также связна [2].
также связна [2].