|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИЛЬБЕРТА СИНГУЛЯРНЫЙ ИНТЕГРАЛЗначение ГИЛЬБЕРТА СИНГУЛЯРНЫЙ ИНТЕГРАЛ в математической энциклопедии: не собственный (в смысле главного значения ио Коши) интеграл
где периодич. функция где Функция Лит.:[1] Нilbеrt D., Grundzuge einer allgemeinen Theorie der linearen Integralgleichungen, Lpz.- В., 1912; [2] Riesz M., "Math. Z..", 1927, Bd 27, № 2, S. 218-44; [3] Бари Н. К., Тригонометрические ряды, М., 1961; [4] Мусхелишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1908. Б. В. Хведелидзе. |
|
|
|


 наз. плотностью Г. с. и., а
наз. плотностью Г. с. и., а  - ядром Г. с. и. Если
- ядром Г. с. и. Если  суммируема, то
суммируема, то  существует почти всюду, а если
существует почти всюду, а если 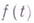 удовлетворяет условию Липшица с показателем
удовлетворяет условию Липшица с показателем  то
то 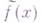 существует при любом sи удовлетворяет тому же условию. Если
существует при любом sи удовлетворяет тому же условию. Если  суммируема с р-й степенью,
суммируема с р-й степенью,  обладает тем же свойством и
обладает тем же свойством и 
 -постоянная, не зависящая от /(л-). Кроме того, имеет место формула обращения Г. с. и.
-постоянная, не зависящая от /(л-). Кроме того, имеет место формула обращения Г. с. и.
 наз. сопряженной с f(x).
наз. сопряженной с f(x).