|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГИЛЬБЕРТА ИНВАРИАНТНЫЙ ИНТЕГРАЛЗначение ГИЛЬБЕРТА ИНВАРИАНТНЫЙ ИНТЕГРАЛ в математической энциклопедии: криволинейный интеграл от замкнутой дифференциальной формы, являющейся производной действия функционала вариационного исчисления. Для функционала ищется вектор-функция не зависел от пути интегрирования. Если такая функция существует, то Г. и. и. наиболее естественным путем воссоединяет теорию Вейерштрасса и теорию Гамильтона-Якоби. Значение Г. и. и. на кривых, соединяющих точки Если кривая При закрепленной точке позволяет записать Г. и. и. в виде при этом Эти соотношения эквивалентны уравнению Гамильтона - Якоби. Интеграл Лит.:[1] Вeltrami Е., "Rend. Ist. Lombardo Sci. Let.", 1868, v. 1, № 2, p. 708-718; [2] Hi1bert D., "Nachr. Ges. Wiss. Gottingen", 1900, S. 253-97; [3] Проблемы Гильберта, М., 1969, с. 57-63; [4] Hilbert D., "Math. Ann.", 1906, Bd 62, S. 351-70; [5] Ахиезер Н. И., Лекции по вариационному исчислению, М., 1955, с. 55-6; [6] Гельфанд И. М., Фомин С. В., Вариационное исчисление, М., 1961, с. 135- 146; [7] Caratheodory С., Variationsrechnung und partielle Differentialgleichungen erster Ordmmg, B.- L., 1935; [8] Янг Л., Лекции по вариационному исчислению и теории оптимального управления, пер. с англ., М., 1974. В. М. Тихомиров. |
|
|
|


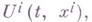 наз. полем, так, чтобы интеграл
наз. полем, так, чтобы интеграл 
 иаз. инвариантным интегралом Гильберта. Условие замкнутости подинтегральной дифференциальной формы порождает систему уравнений с частными производными 1-го порядка.
иаз. инвариантным интегралом Гильберта. Условие замкнутости подинтегральной дифференциальной формы порождает систему уравнений с частными производными 1-го порядка. и
и  , становится, в силу инвариантности
, становится, в силу инвариантности  , функцией
, функцией  этой пары точек и наз. действием. Линия уровня
этой пары точек и наз. действием. Линия уровня  наз. трансверсалями поля
наз. трансверсалями поля  . Решения уравнения
. Решения уравнения  являются экстремалями функционала
являются экстремалями функционала  . Обратно, если нек-рая область покрыта полем экстремалей, то интеграл
. Обратно, если нек-рая область покрыта полем экстремалей, то интеграл  , построенный по функции
, построенный по функции  , равной производной экстремали, проходящей через
, равной производной экстремали, проходящей через 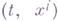 , есть Г. и. и. Возможность подобного окружения, а значит, и построения Г. и. и., формулируется обычно в виде Якоби условия.
, есть Г. и. и. Возможность подобного окружения, а значит, и построения Г. и. и., формулируется обычно в виде Якоби условия. проходит в области, покрытой полем, через точки
проходит в области, покрытой полем, через точки  и
и  , соединенные также экстремалью
, соединенные также экстремалью  , то инвариантность Г. и. и. и равенство
, то инвариантность Г. и. и. и равенство  позволяют получить Вейерштрасса формулу для приращения функционала, а следовательно, и достаточное Вейерштрасса условие экстремума.
позволяют получить Вейерштрасса формулу для приращения функционала, а следовательно, и достаточное Вейерштрасса условие экстремума. действие
действие  есть функция
есть функция  точки
точки  и
и  Переход, к каноническим координатам
Переход, к каноническим координатам 


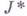 для поля геодезических был введен Э. Бельтрами [1] в 1868, а в общем случае - Д. Гильбертом [2] - [4] в 1900.
для поля геодезических был введен Э. Бельтрами [1] в 1868, а в общем случае - Д. Гильбертом [2] - [4] в 1900.