|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЕОДЕЗИЧЕСКОЕ РАССТОЯНИЕЗначение ГЕОДЕЗИЧЕСКОЕ РАССТОЯНИЕ в математической энциклопедии: длина кратчайшей геодезической линии, соединяющей две точки (или два множества). В вариационном исчислении Г. р.- значение исследуемого функционала на экстремали, соединяющей две рассматриваемые точки. ГЕОКРИОЛОГИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ - математич. задачи, возникающие при изучении процессов и явлений, происходящих в мерзлых почвах и горных породах, географич. распространения и условий формирования сезонномерзлых и многолетнемерзлых горных пород (вечной мерзлоты). Интересные Г. м. з. возникают при изучении проблемы взаимодействия температурных и влажностных полей в зонах с подвижными границами раздела фаз. Характерной особенностью Г. м. з. является то, что процессы тепло- и массообмена, происходящие при промерзании и оттаивании пород, тесно связаны между собой. Задача сводится к системе квазилинейных уравнений параболич. типа, поскольку тепло- и влагообменные характеристики среды существенно зависят от искомых функций. Типичными примерами подобных задач являются исследование промерзания влагонасыщенных тонкодисперсных пород, к-рое сопровождается миграцией влаги к фронту промерзания н пучением, а также исследование оттаивания грубодисперсных пород, сопряженное с инфильтрацией и фильтрацией влаги. Особое значение для инженерной геологии имеет решение многомерной Стефана задачи, для областей со сложной конфигурацией, в частности о чаше протанвання при гражданском и промышленном строительстве. Решение вопросов истории, геокриологпи приводит к необходимости исследования многофронтовой задачи Стефана с учетом образования зон и вырождения их в точку. Важное значение при этом имеет увязка процессов промерзания и оттаивания в верхних слоях литосферы с радиационно-тепло-вым балансом. В. <И. Дмитриев. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ - последовательность чисел, каждое из к-рых равно предыдущему, умноженному на нек-рое постоянное для данной прогрессии число
а сумма первых пчленов Г. п. (знаменатель к-рой не равен 1) - формулой Если - простейший пример сходящегося ряда -геометрический ряд, число Термин "Г. п." связан со свойством любого члена Г. п. с положительными членами: |
|
|
|

 (знаменатель прогрессии). Г. п. наз. возрастающей, если
(знаменатель прогрессии). Г. п. наз. возрастающей, если  , убывающей, если
, убывающей, если  ; если
; если  , то Г. п.- знакочередующаяся. Любой член Г. п.
, то Г. п.- знакочередующаяся. Любой член Г. п. 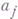 выражается через ее первый член
выражается через ее первый член 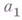 и знаменатель
и знаменатель  формулой
формулой

 , то при неограниченном возрастании числа псумма
, то при неограниченном возрастании числа псумма  стремится к пределу
стремится к пределу 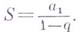 Это число
Это число 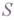 наз. суммой бесконечно убывающей геометрической прогрессии. Выражение
наз. суммой бесконечно убывающей геометрической прогрессии. Выражение 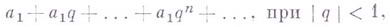
 является суммой геометрии, ряда.
является суммой геометрии, ряда. т. е. любой член есть геометрическое среднее между предыдущим и последующим ее членами, о. А. Иванова.
т. е. любой член есть геометрическое среднее между предыдущим и последующим ее членами, о. А. Иванова.