|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЕОДЕЗИЧЕСКАЯ КРИВИЗНАЗначение ГЕОДЕЗИЧЕСКАЯ КРИВИЗНА в математической энциклопедии: в точке кривой где штрих означает дифференцирование по t. Г. к. входит в выражение вариации длины Интегральной Г. к., или поворотом кривой Связь поворота замкнутого контура с интегральной кривизной охваченной им области на поверхности дает Гаусса - Бонне теорема. Г. к. принадлежит внутренней геометрии поверхности и допускает выражение через метрич. тензор и производные внутренних координат поверхности по параметру tкривой. Если внутренняя геометрия ри-манова пространства изучается в отвлечении от возможных погружений, то Г. к. остается единственной кривизной кривой и слово "геодезическая" опускается. При рассмотрении кривых в подмногообразии риманова пространства кривизна кривой может определяться во внешнем пространстве и в подмногообразии, подобно тому, как на поверхности кривая имеет обычную кривизну и Г. к. Можно ввести понятие Г. к. для кривой у на общей выпуклой поверхности. Если кривая g. имеет длину и каждая ее дуга имеет определенный поворот, то правой (левой) Г. к. кривой g. в точке x наз. предел отношения правого (левого) поворота дуги кривой к ее длине, при условии, что дуга стягивается в точку х. В финслеровом пространстве определяют два понятия Г. к., различающиеся способом измерения длины вектора, заменяющего v. На геодезических эти Г. к. равны нулю. Ю, C. Слобовян. |
|
|
|

 на поверхности
на поверхности  - скорость вращения касательной к
- скорость вращения касательной к  вокруг нормали
вокруг нормали  к
к  , т. е. проекция на
, т. е. проекция на  вектора угловой скорости вращения касательной при движении вдоль
вектора угловой скорости вращения касательной при движении вдоль  . Предполагается, что
. Предполагается, что 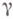 и
и  регулярны и ориентированы, скорость берется относительно длины
регулярны и ориентированы, скорость берется относительно длины  вдоль
вдоль  . Г. к. может быть определена как кривизна проекции
. Г. к. может быть определена как кривизна проекции  на касательную плоскость к Fв рассматриваемой точке. Г. к. равна
на касательную плоскость к Fв рассматриваемой точке. Г. к. равна 
 при варьировании
при варьировании  на
на  . При закрепленных концах:
. При закрепленных концах:
 - вектор вариации кривой. Кривые, на к-рых
- вектор вариации кривой. Кривые, на к-рых 
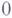 - геодезические линии.
- геодезические линии. , наз. интеграл
, наз. интеграл 