|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЕОДЕЗИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИЗначение ГЕОДЕЗИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ в математической энциклопедии: задачи, связанные с определением гравитационного поля и фигуры Земли в единой системе координат. Используют декартову прямоугольную систему где Фигуру Земли и ее поле определяют по измерениям геометрич. характера (расстояний между точками, углов между направлениями), измерениям силы тяжести, локации Луны, наблюдениям искусственных спутников Земли и внегалактических радиоисточников. При развитии наземной сети геодезич. измерений необходимо определять элементы ориентировки местных систем координат. В выводах с внеземными данными большое значение приобретают геодезич. построения без отвеса (см. [1]). Эти построения основаны на синхронном фотографировании с нескольких пунктов подвижной цели на фоне звезд. Если известны координаты части пунктов и известны склонения и прямые восхождения звезд, сфотографированных вместе с целью, то возможно вывести координаты как сфотографированных целей, так и неизвестные координаты пунктов. В наземном варианте, из-за искажений углов в вертикальных плоскостях влиянием атмосферной рефракции для вывода высот Нточек земной поверхности, разработаны методы, связанные с использованием силы тяжести. Этими же методами определяют земное гравитационное попе. Современная теория использования силы тяжести в геодезии принадлежит М. С. Молоденскому (см. [2]). Эта теория основана на решении краевой задачи с косой производной для уравнения Лапласа. Отсчетным может служить поле потенциала Uпритяжения близкого к земному. Здесь где Здесь Решение задачи сводится к выводу плотности простого слоя также на земной поверхности, связанного с потенциалом Тнек-рой зависимостью. Из этой зависимости и краевого условия выводится сингулярное интегральное уравнение 2-го рода. На это уравнение при определенных условиях распространяется альтернатива Фредгольма. Краевые условия допускают единственное решение при эллипсоидальном отсчетном поле. Если же отсчетное поле вырождается в сферическое, решением задачи становится произвольная сферич. функция 1-й степени. Из-за неизбежных ошибок измерений вводят дополнительные условия о совмещении центра инерции Земли и центра отсчетного эллипсоида, о параллельности полярной главной центральной оси инерции Земли и малой оси отсчетного эллипсоида. Центр инерции Земли может не лежать на ее оси вращения. В частности, так будет, если из гравитационного поля Земли для уменьшения ошибок интерполяции силы тяжести выделено влияние топографич. масс. В горных районах, из-за сложности земной поверхности, численное решение представляет большие практич. затруднения. Координаты Величину Из исследования орбит искусственных спутников Земли определяют отличия ее гравитационного поля от сферического, как правило, через вывод коэффициентов разложения потенциала по сферич. функциям. Традиционные методы небесной механики дополняет теория совместного определения гравитационного поля и координат станций наблюдения за спутниками. Основы математич. теории фигуры Земли заложены И. Ньютоном (I. Newton, 1687), вычислившим сжатие земного эллипсоида при условии, что он однороден по плотности. А. Клеро (A. Clairaut, 1743) в первом приближении исследовал гравитационное поле неоднородной Земли, вращающейся в гидростатич. равновесии. Л. Эйлер (L. Euler, 1757) заложил основы теории уровенных поверхностей земного потенциала. Изучая притяжение небесных тел - сфероидов, в частности эллипсоидов вращения, П. Лаплас (P. Laplace, 1785) обобщил результаты А. Клеро о распределении силы тяжести на поверхности планеты, освободив их от предположения о гидростатич. равновесии и сохранив точность вывода А. Клеро (порядка земного сжатия - 1 : 300). При этом П. Лаплас развил теорию сферич. функций и рядов. Работы Дж. Стокса (G. Stokes), развитые и дополненные в дальнейшем многими геодезистами, служили теоретич. основой использования гравиметрич. измерений в геодезии до появления работ М. С. Молоденского. К определению фигуры Земли Дж. Стоке впервые подошел как к краевой задаче, приближенно решив первую краевую задачу для сфероида и обосновав результаты А. Клеро и П. Лапласа. Это решение Дж. Стокса опередило результаты П. Дирихле (P. Dirichlet, 1852) по решению такой задачи для сферы разложением по сферич. функциям. Дж. Стоке (1849) выразил также высоту внешней уровенной поверхности планеты над сфероидом через силу тяжести на поверхности планеты. Вывод о возможности замены притяжения тела притяжением простого слоя на поверхности тела сделан К. Гауссом (С. .Gauss, 1840). Теория вращения неоднородной жидкости в гидростатич. равновесии имеет значение при совместном решении геофизич. и геодезич. задач. Основные результаты в этой области принадлежат А. М. Ляпунову. Лит.:[1] Изотов А. А. и др., Основы спутниковой геодезии, М., 1974; [2] Молоденский М. С., Еремеев В. Ф., Юркина М. И., Методы изучения внешнего гравитационного поля и фигуры Земли, М., I960; [3] Морозов В. П., Курс сфероидической геодезии, М., 1969. В. Ф. Еремеев. М. И. Юркина. |
|
|
|

 а также криволинейные ортогональные координаты В, L, H (см. [3]) или
а также криволинейные ортогональные координаты В, L, H (см. [3]) или  связанные с сжатым эллипсоидом вращения (из-за близости фигуры Земли к такому эллипсоиду). При этом
связанные с сжатым эллипсоидом вращения (из-за близости фигуры Земли к такому эллипсоиду). При этом 
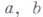 - большая и малая полуоси эллипсоида, 2с - его фокусное расстояние
- большая и малая полуоси эллипсоида, 2с - его фокусное расстояние 

 - гравитационная постоянная, т - масса, близкая к массе Земли,
- гравитационная постоянная, т - масса, близкая к массе Земли,  - угловая скорость ее вращения,
- угловая скорость ее вращения,  - функции Ле-жандра соответственно 1-го и 2-го рода. Потенциал
- функции Ле-жандра соответственно 1-го и 2-го рода. Потенциал  силы тяжести выражается через его значение
силы тяжести выражается через его значение  в начале счета высот (уровня моря) и приращение, выводимое из геометрич. нивелирования и измерений силы тяжести вдоль .его линии:
в начале счета высот (уровня моря) и приращение, выводимое из геометрич. нивелирования и измерений силы тяжести вдоль .его линии:
 - элементарное нивелирное превышение. По приращению
- элементарное нивелирное превышение. По приращению  потенциала определяют приближенную координату
потенциала определяют приближенную координату  , полагая, что нивелирование выполнено в поле потенциала силы тяжести эллипсоида, уровенного относительно этого потенциала. Для уточнения координаты
, полагая, что нивелирование выполнено в поле потенциала силы тяжести эллипсоида, уровенного относительно этого потенциала. Для уточнения координаты  (вывода высоты Н).и определения внешнего земного гравитационного поля достаточно найти потенциал Т, наз. возмущающим:
(вывода высоты Н).и определения внешнего земного гравитационного поля достаточно найти потенциал Т, наз. возмущающим:
 - потенциал центробежной силы, возникающий из-за вращения Земли. Краевое условие на земной поверхности для вывода потенциала получают, используя связь
- потенциал центробежной силы, возникающий из-за вращения Земли. Краевое условие на земной поверхности для вывода потенциала получают, используя связь  и вычисляя
и вычисляя  в точке с координатой
в точке с координатой  . На бесконечности
. На бесконечности  потенциал Тудовлетворяет условию
потенциал Тудовлетворяет условию  .
. нек-рой точки, принимаемой за исходную при обработке измерений геометрич. характера, назначают заранее произвольно, но так, чтобы компоненты
нек-рой точки, принимаемой за исходную при обработке измерений геометрич. характера, назначают заранее произвольно, но так, чтобы компоненты  уклонения отвеса от нормали к эллипсоиду были малы. При этом вводят условия о параллельности осей вращения Земли и эллипсоида и плоскостей начальных астрономич. и геодезия, меридианов.
уклонения отвеса от нормали к эллипсоиду были малы. При этом вводят условия о параллельности осей вращения Земли и эллипсоида и плоскостей начальных астрономич. и геодезия, меридианов. и координаты центра инерции Земли определяют, сопоставляя решение упомянутого интегрального уравнения с наблюдениями астрономич. широт
и координаты центра инерции Земли определяют, сопоставляя решение упомянутого интегрального уравнения с наблюдениями астрономич. широт  и долгот
и долгот  и с высотами Н, выводимыми из геометрич. и астрономо-гравиметрич. нивелирования.
и с высотами Н, выводимыми из геометрич. и астрономо-гравиметрич. нивелирования.