"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГЁЛЬДЕРОВО ПРОСТРАНСТВОЗначение ГЁЛЬДЕРОВО ПРОСТРАНСТВО в математической энциклопедии:
банахово пространство ограниченных и непрерывных функций  , определенных на множестве Е n-мерного евклидова пространства и удовлетворяющих на Е Гёльдера условию. , определенных на множестве Е n-мерного евклидова пространства и удовлетворяющих на Е Гёльдера условию.
Г. п. 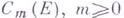 - целое, состоит из траз непрерывно дифференцируемых на Ефункций (непрерывных при т=0). - целое, состоит из траз непрерывно дифференцируемых на Ефункций (непрерывных при т=0).
Г. п.  - целое, состоит из функций, траз непрерывно дифференцируемых (непрерывных при т = 0), все т-е производные к-рых удовлетворяют условию Гёльдера с показателем - целое, состоит из функций, траз непрерывно дифференцируемых (непрерывных при т = 0), все т-е производные к-рых удовлетворяют условию Гёльдера с показателем  . .
Норма в  вводится следующим образом: вводится следующим образом:

где  - целые, - целые,

Основные свойства Г. п. для ограниченной связной области ( - замыкание - замыкание  ): ):
1)  вложено в вложено в  , если , если   , k, т - целые, , k, т - целые, 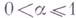 , ,  . При этом . При этом  и постоянная Ане зависит от и постоянная Ане зависит от  . .
2) Единичный шар пространства  компактен в компактен в  , если , если  . Следовательно, любое ограниченное множество функций из . Следовательно, любое ограниченное множество функций из  содержит последовательность функций, сходящихся в метрике содержит последовательность функций, сходящихся в метрике  к функции пространства к функции пространства  . .
Лит.: [1] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957.
Л. П. Купцов.
|

 , определенных на множестве Е n-мерного евклидова пространства и удовлетворяющих на Е Гёльдера условию.
, определенных на множестве Е n-мерного евклидова пространства и удовлетворяющих на Е Гёльдера условию.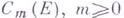 - целое, состоит из траз непрерывно дифференцируемых на Ефункций (непрерывных при т=0).
- целое, состоит из траз непрерывно дифференцируемых на Ефункций (непрерывных при т=0). - целое, состоит из функций, траз непрерывно дифференцируемых (непрерывных при т = 0), все т-е производные к-рых удовлетворяют условию Гёльдера с показателем
- целое, состоит из функций, траз непрерывно дифференцируемых (непрерывных при т = 0), все т-е производные к-рых удовлетворяют условию Гёльдера с показателем  .
. вводится следующим образом:
вводится следующим образом:
 - целые,
- целые,
 - замыкание
- замыкание  ):
): вложено в
вложено в  , если
, если 
 , k, т - целые,
, k, т - целые, 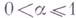 ,
,  . При этом
. При этом  и постоянная Ане зависит от
и постоянная Ане зависит от  .
. компактен в
компактен в  , если
, если  . Следовательно, любое ограниченное множество функций из
. Следовательно, любое ограниченное множество функций из  содержит последовательность функций, сходящихся в метрике
содержит последовательность функций, сходящихся в метрике  к функции пространства
к функции пространства  .
.