" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ГЁЛЬДЕРА МЕТОДЫ СУММИРОВАНИЯ

Значение ГЁЛЬДЕРА МЕТОДЫ СУММИРОВАНИЯ в математической энциклопедии:

совокупность методов суммирования числовых рядов; введены О. Гёльдером [1] как обобщение средних арифметических метода суммирования. Ряд

суммируется методом Гёльдера ( Н, k) к сумме s, если

где

В частности, -суммируемость ряда означает его обычную сходимость; есть метод средних арифметических. Методы - вполне регулярные методы, суммирования при любом kи совместны для всех k(см. Совместность методов суммирования). С увеличением kсила метода возрастает: если ряд суммируем методом 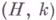к сумме s, то он суммируем к той же сумме методом при любом Метод при всех kравносилен и совместен с Чезаро методом суммирования того же порядка k. Если ряд суммируем методом , то его члены необходимо удовлетворяют условию .

Лит.:[1] Holder О., "Math. Ann.", 1882, Bd 20, S. 535- 549; [2] Xapди Г., Расходящиеся ряды, пер. с англ., М., 1951.

И. И. Волков.