"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАУССА РАЗЛОЖЕНИЕ
Значение ГАУССА РАЗЛОЖЕНИЕ в математической энциклопедии:
топологической группыС- представление всюду плотного подмножества  в виде
в виде 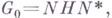 где Н - абелева подгруппа группы
где Н - абелева подгруппа группы  - нильпотентные подгруппы группы G, нормализуемые Н. Если G - группа
- нильпотентные подгруппы группы G, нормализуемые Н. Если G - группа  невырожденных вещественных матриц m-го порядка, Н - подгруппа диагональных матриц, N(соответственно
невырожденных вещественных матриц m-го порядка, Н - подгруппа диагональных матриц, N(соответственно  ) - подгруппа нижне (верхне)-треугольных матриц с единицами на главной диагонали,
) - подгруппа нижне (верхне)-треугольных матриц с единицами на главной диагонали,  - подмножество матриц из G, все главные миноры к-рых отличны от нуля, то разложение
- подмножество матриц из G, все главные миноры к-рых отличны от нуля, то разложение  наз. разложением Гаусса полной линейной группы и непосредственно связано с Гаусса методом решения систем линейных уравнений: если
наз. разложением Гаусса полной линейной группы и непосредственно связано с Гаусса методом решения систем линейных уравнений: если  где
где  - невырожденная матрица коэффициентов системы линейных уравнений
- невырожденная матрица коэффициентов системы линейных уравнений  то приведение матрицы
то приведение матрицы 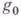 методом Гаусса к треугольному виду
методом Гаусса к треугольному виду  , можно осуществить умножением g0 слева на нижнетреугольную матрицу
, можно осуществить умножением g0 слева на нижнетреугольную матрицу  Строгое определение разложения Гаусса требует введения следующих терминов. Пусть G- топо-логич. группа, Н - ее подгруппа,
Строгое определение разложения Гаусса требует введения следующих терминов. Пусть G- топо-логич. группа, Н - ее подгруппа,  - нильпотентные подгруппы в G, нормализуемые Н. Подгруппа Нназ. треугольным усечением группы, если а)
- нильпотентные подгруппы в G, нормализуемые Н. Подгруппа Нназ. треугольным усечением группы, если а)  где
где  - коммутант группы
- коммутант группы  - связные разрешимые подгруппы группы G;б) множество
- связные разрешимые подгруппы группы G;б) множество 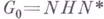 всюду плотно в G, и разложение
всюду плотно в G, и разложение  однозначно. Разложение
однозначно. Разложение  наз. треугольным разложением в G. Если Н - абелева группа, то это разложение наз. вполне треугольным разложением, или разложением Гаусса. В этом случае подгруппы
наз. треугольным разложением в G. Если Н - абелева группа, то это разложение наз. вполне треугольным разложением, или разложением Гаусса. В этом случае подгруппы  разрешимы.
разрешимы.
Пусть  - неприводимое (непрерывное) представление группы
- неприводимое (непрерывное) представление группы  в конечномерном векторном пространстве
в конечномерном векторном пространстве  - подпространство всех векторов из V, неподвижных относительно
- подпространство всех векторов из V, неподвижных относительно 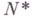 ; тогда
; тогда  инвариантно относительно Н, и представление
инвариантно относительно Н, и представление  группы
группы  в
в 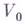 неприводимо. Представление
неприводимо. Представление  определяет
определяет  однозначно с точностью до эквивалентности. Представление
однозначно с точностью до эквивалентности. Представление 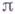 содержится (как инвариантная часть) в представлении
содержится (как инвариантная часть) в представлении  группы
группы  , индуцированном представлением
, индуцированном представлением  , подгруппы Вв классе
, подгруппы Вв классе  , где
, где  - продолжение на Водноименного представления группы H, тривиальное на N. При этом пространство
- продолжение на Водноименного представления группы H, тривиальное на N. При этом пространство  одномерно. Если Н - абелева подгруппа, то
одномерно. Если Н - абелева подгруппа, то  одномерно и
одномерно и  - характер группы Н. Известны следующие примеры треугольных разложений групп Ли. 1) Пусть G - редук-тивная связная комплексная группа Ли с картановской подалгеброй
- характер группы Н. Известны следующие примеры треугольных разложений групп Ли. 1) Пусть G - редук-тивная связная комплексная группа Ли с картановской подалгеброй  - редуктивная связная подгруппа в G, содержащая
- редуктивная связная подгруппа в G, содержащая 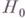 . Тогда подгруппа Нявляется треугольным усечением группы G.2) Пусть G - редуктивная связная линейная группа Ли; тогда группа G содержит треугольное усечение
. Тогда подгруппа Нявляется треугольным усечением группы G.2) Пусть G - редуктивная связная линейная группа Ли; тогда группа G содержит треугольное усечение  , где А - од-носвязная абелева подгруппа в G (порождаемая некомпактными корнями в алгебре Ли группы G), M - централизатор Ав максимальной компактной подгруппе
, где А - од-носвязная абелева подгруппа в G (порождаемая некомпактными корнями в алгебре Ли группы G), M - централизатор Ав максимальной компактной подгруппе  . 3) В частности, всякая редуктивная связная комплексная группа Ли допускает Г. р.
. 3) В частности, всякая редуктивная связная комплексная группа Ли допускает Г. р.  , где Н - картановская подгруппа в группе G; Nсоответственно
, где Н - картановская подгруппа в группе G; Nсоответственно  - аналитич. одгруппа в G, алгебра Ли к-рой натянута на все корневые векторы
- аналитич. одгруппа в G, алгебра Ли к-рой натянута на все корневые векторы 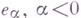 (соответственно
(соответственно  ),
),  - корень относительно Н, т. е.
- корень относительно Н, т. е.  и
и  являются противоположными Бореля подгруппами. В примерах 1) - 3) подгруппы
являются противоположными Бореля подгруппами. В примерах 1) - 3) подгруппы 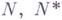 од-носвязны,
од-носвязны, 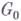 открыто в G в топологии Зариского, а отображение
открыто в G в топологии Зариского, а отображение  является изоморфизмом алгебраич. многообразий (и, в частности, гомеоморфизмом). Этот факт позволяет доказать, что алгебраич. многообразие G рационально.
является изоморфизмом алгебраич. многообразий (и, в частности, гомеоморфизмом). Этот факт позволяет доказать, что алгебраич. многообразие G рационально.
Лит.:[1] Желобенко Д. П., Компактные группы Ли и их представления, М., 1968. Д. П. Желобенко.

 в виде
в виде 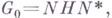 где Н - абелева подгруппа группы
где Н - абелева подгруппа группы  - нильпотентные подгруппы группы G, нормализуемые Н. Если G - группа
- нильпотентные подгруппы группы G, нормализуемые Н. Если G - группа  невырожденных вещественных матриц m-го порядка, Н - подгруппа диагональных матриц, N(соответственно
невырожденных вещественных матриц m-го порядка, Н - подгруппа диагональных матриц, N(соответственно  ) - подгруппа нижне (верхне)-треугольных матриц с единицами на главной диагонали,
) - подгруппа нижне (верхне)-треугольных матриц с единицами на главной диагонали,  - подмножество матриц из G, все главные миноры к-рых отличны от нуля, то разложение
- подмножество матриц из G, все главные миноры к-рых отличны от нуля, то разложение  наз. разложением Гаусса полной линейной группы и непосредственно связано с Гаусса методом решения систем линейных уравнений: если
наз. разложением Гаусса полной линейной группы и непосредственно связано с Гаусса методом решения систем линейных уравнений: если  где
где  - невырожденная матрица коэффициентов системы линейных уравнений
- невырожденная матрица коэффициентов системы линейных уравнений  то приведение матрицы
то приведение матрицы 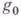 методом Гаусса к треугольному виду
методом Гаусса к треугольному виду  , можно осуществить умножением g0 слева на нижнетреугольную матрицу
, можно осуществить умножением g0 слева на нижнетреугольную матрицу  Строгое определение разложения Гаусса требует введения следующих терминов. Пусть G- топо-логич. группа, Н - ее подгруппа,
Строгое определение разложения Гаусса требует введения следующих терминов. Пусть G- топо-логич. группа, Н - ее подгруппа,  - нильпотентные подгруппы в G, нормализуемые Н. Подгруппа Нназ. треугольным усечением группы, если а)
- нильпотентные подгруппы в G, нормализуемые Н. Подгруппа Нназ. треугольным усечением группы, если а)  где
где  - коммутант группы
- коммутант группы  - связные разрешимые подгруппы группы G;б) множество
- связные разрешимые подгруппы группы G;б) множество 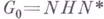 всюду плотно в G, и разложение
всюду плотно в G, и разложение  однозначно. Разложение
однозначно. Разложение  наз. треугольным разложением в G. Если Н - абелева группа, то это разложение наз. вполне треугольным разложением, или разложением Гаусса. В этом случае подгруппы
наз. треугольным разложением в G. Если Н - абелева группа, то это разложение наз. вполне треугольным разложением, или разложением Гаусса. В этом случае подгруппы  разрешимы.
разрешимы. - неприводимое (непрерывное) представление группы
- неприводимое (непрерывное) представление группы  в конечномерном векторном пространстве
в конечномерном векторном пространстве  - подпространство всех векторов из V, неподвижных относительно
- подпространство всех векторов из V, неподвижных относительно 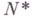 ; тогда
; тогда  инвариантно относительно Н, и представление
инвариантно относительно Н, и представление  группы
группы  в
в 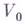 неприводимо. Представление
неприводимо. Представление  определяет
определяет  однозначно с точностью до эквивалентности. Представление
однозначно с точностью до эквивалентности. Представление 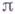 содержится (как инвариантная часть) в представлении
содержится (как инвариантная часть) в представлении  группы
группы  , индуцированном представлением
, индуцированном представлением  , подгруппы Вв классе
, подгруппы Вв классе  , где
, где  - продолжение на Водноименного представления группы H, тривиальное на N. При этом пространство
- продолжение на Водноименного представления группы H, тривиальное на N. При этом пространство  одномерно. Если Н - абелева подгруппа, то
одномерно. Если Н - абелева подгруппа, то  одномерно и
одномерно и  - характер группы Н. Известны следующие примеры треугольных разложений групп Ли. 1) Пусть G - редук-тивная связная комплексная группа Ли с картановской подалгеброй
- характер группы Н. Известны следующие примеры треугольных разложений групп Ли. 1) Пусть G - редук-тивная связная комплексная группа Ли с картановской подалгеброй  - редуктивная связная подгруппа в G, содержащая
- редуктивная связная подгруппа в G, содержащая 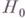 . Тогда подгруппа Нявляется треугольным усечением группы G.2) Пусть G - редуктивная связная линейная группа Ли; тогда группа G содержит треугольное усечение
. Тогда подгруппа Нявляется треугольным усечением группы G.2) Пусть G - редуктивная связная линейная группа Ли; тогда группа G содержит треугольное усечение  , где А - од-носвязная абелева подгруппа в G (порождаемая некомпактными корнями в алгебре Ли группы G), M - централизатор Ав максимальной компактной подгруппе
, где А - од-носвязная абелева подгруппа в G (порождаемая некомпактными корнями в алгебре Ли группы G), M - централизатор Ав максимальной компактной подгруппе  . 3) В частности, всякая редуктивная связная комплексная группа Ли допускает Г. р.
. 3) В частности, всякая редуктивная связная комплексная группа Ли допускает Г. р.  , где Н - картановская подгруппа в группе G; Nсоответственно
, где Н - картановская подгруппа в группе G; Nсоответственно  - аналитич. одгруппа в G, алгебра Ли к-рой натянута на все корневые векторы
- аналитич. одгруппа в G, алгебра Ли к-рой натянута на все корневые векторы 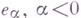 (соответственно
(соответственно  ),
),  - корень относительно Н, т. е.
- корень относительно Н, т. е.  и
и  являются противоположными Бореля подгруппами. В примерах 1) - 3) подгруппы
являются противоположными Бореля подгруппами. В примерах 1) - 3) подгруппы 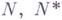 од-носвязны,
од-носвязны, 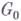 открыто в G в топологии Зариского, а отображение
открыто в G в топологии Зариского, а отображение  является изоморфизмом алгебраич. многообразий (и, в частности, гомеоморфизмом). Этот факт позволяет доказать, что алгебраич. многообразие G рационально.
является изоморфизмом алгебраич. многообразий (и, в частности, гомеоморфизмом). Этот факт позволяет доказать, что алгебраич. многообразие G рационально.