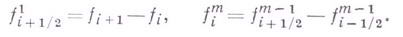|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАУССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛАЗначение ГАУССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА в математической энциклопедии: формула, использующая в качестве узлов интерполяции ближайшие к точке интерполирования хузлы. Если написанная по узлам написанная по узлам Преимущество Г. и. ф. состоит в том, что указанный выбор узлов интерполяции обеспечивает наилучшую оценку остаточного члена по сравнению с любым другим выбором, а упорядоченность узлов по мере их близости к точке интерполяции уменьшает вычислительную погрешность интерполирования. Лит.:[1] Березин И. С., Жидков Н. П., Методы вычислений, т. 1, 3 изд., М., 1966; [2] Бахвалов Н. С., Численные методы, М., 1973. М. К. Самарин. |
|
|
|

 то формула
то формула 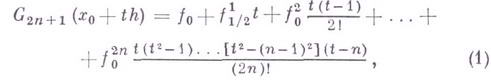
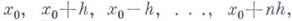
 наз. формулой Гаусса для интерполирования вперед, а формула
наз. формулой Гаусса для интерполирования вперед, а формула 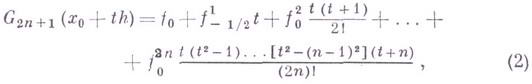
 наз. формулой Гаусса для интерполирования назад (см. [1], [2]). В формулах (1) и (2) использованы конечные разности, определяемые следующим образом:
наз. формулой Гаусса для интерполирования назад (см. [1], [2]). В формулах (1) и (2) использованы конечные разности, определяемые следующим образом: