|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГАУССА ВАРИАЦИОННАЯ ЗАДАЧАЗначение ГАУССА ВАРИАЦИОННАЯ ЗАДАЧА в математической энциклопедии: - вариационная задача, исследованная впервые К. Гауссом [1] и в современных терминах формулируемая следующим образом. Пусть - ньютонов потенциал меры
представляющему собой скалярное произведение Значение Г. в. з. определяется тем, что равновесная мера (см. Робена задача).может быть получена как решение Г. в. з. при определенном выборе меры и.; напр., можно принять за Лит.:[1] Gauss С. F., Werke, Bd 5, Gott., 1867, S. 195-242; [2] Ландкоф Н. С., Основы современной теории потенциала, М., 1966, гл. 2; [3] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964, гл. 11. Е. Д. Соломенцев. |
|
|
|
- положительная мера в евклидовом пространстве 
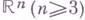, имеющая конечную энергию (см. Энергия мер), и пусть 
. Требуется среди всех мер 
с компактным носителем 
найти такую меру 
, к-рая дает минимум интегралу 
в предгильбертовом пространстве мер.
равномерное распределение массы на сфере с центром в начале координат, охватывающей множество К.