|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛГЕБРА МНОЖЕСТВЗначение АЛГЕБРА МНОЖЕСТВ в математической энциклопедии: - непустая совокупность подмножеств нек-рого множества W, замкнутая относительно теоретико-множественных операций (объединения, пересечения, образования дополнения), производимых в конечном числе. Для того чтобы нек-рый класс подмножеств множества W был А. м., достаточно (и необходимо), чтобы он был замкнут относительно образования объединений и дополнений. А. м., замкнутая относительно образования счетных объединений, наз. Примеры. 1) Совокупность конечных подмножеств произвольного множества W и дополнений к ним есть А. м.; совокупность не более чем счетных подмножеств W и дополнений к ним есть 2) Совокупность конечных объединений интервалов вида
образует А. м. 3) W- топологич. пространство; 4) где Е- борелевское подмножество 5) Совокупность измеримых по Лебегу подмножеств Алгебры (соответственно Лит.:[1] Данфорд Н., Шварц Д ж., Линейные операторы. Общая теория, пер. с англ., М., 1962; [2] Xалмош П., Теория меры, пер. с англ., М., 1953; [3] Невё Ж., Математические основы теории вероятностей, пер. с франц., М., 1969. В. В. Сазонов. |
|
|
|

 -алгеброй множеств (
-алгеброй множеств ( -А. <м.). Всякая
-А. <м.). Всякая  -А. м. замкнута относительно теоретико-множественных операций, производимых в счетном числе.
-А. м. замкнута относительно теоретико-множественных операций, производимых в счетном числе. -А. м.
-А. м.
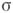 -А. м. В, порожденная открытыми подмножествами W (иными словами, наименьшая
-А. м. В, порожденная открытыми подмножествами W (иными словами, наименьшая  -А. м., содержащая все открытые подмножества W), наз. борелевской
-А. м., содержащая все открытые подмножества W), наз. борелевской  -алгеброй подмножеств W, а множества, принадлежащие В, наз. борелевскими множествами.
-алгеброй подмножеств W, а множества, принадлежащие В, наз. борелевскими множествами. где Т- произвольное множество (т. е. W - множество всех действительных функций на Т);класс Амножеств вида
где Т- произвольное множество (т. е. W - множество всех действительных функций на Т);класс Амножеств вида 
 , образует А. м.; в теории случайных процессов вероятностная мера часто задается первоначально лишь для множеств из алгебры этого типа и затем доопределяется на более широком классе множеств (на
, образует А. м.; в теории случайных процессов вероятностная мера часто задается первоначально лишь для множеств из алгебры этого типа и затем доопределяется на более широком классе множеств (на  -алгебре, порожденной А).
-алгебре, порожденной А). образует
образует 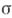 -А. м.
-А. м. -алгебры) являются естественной областью определения конечно аддитивных (соответственно
-алгебры) являются естественной областью определения конечно аддитивных (соответственно  -аддитивных) мер. По теореме о продолжении меры всякая
-аддитивных) мер. По теореме о продолжении меры всякая  -конечная
-конечная  -аддитивная мера, заданная на алгебре А, может быть однозначно продолжена до
-аддитивная мера, заданная на алгебре А, может быть однозначно продолжена до  -аддитивной меры, определенной на
-аддитивной меры, определенной на  -алгебре, порожденной А.
-алгебре, порожденной А.